Derivative of y=tg√2x/x+1

The solution

You have entered [src]

   /  _____\    
tan\\/ 2*x /    
------------ + 1
     x

$$1 + \frac{\tan{\left(\sqrt{2 x} \right)}}{x}$$

  /   /  _____\    \
d |tan\\/ 2*x /    |
--|------------ + 1|
dx\     x          /

$$\frac{d}{d x} \left(1 + \frac{\tan{\left(\sqrt{2 x} \right)}}{x}\right)$$

Transform

Detail solution

Differentiate $1 + \frac{\tan{\left(\sqrt{2 x} \right)}}{x}$ term by term:
1. Apply the quotient rule, which is:
  
  $\frac{d}{d x} \frac{f{\left(x \right)}}{g{\left(x \right)}} = \frac{- f{\left(x \right)} \frac{d}{d x} g{\left(x \right)} + g{\left(x \right)} \frac{d}{d x} f{\left(x \right)}}{g^{2}{\left(x \right)}}$
  
  $f{\left(x \right)} = \tan{\left(\sqrt{2 x} \right)}$ and $g{\left(x \right)} = x$ .
  
  To find $\frac{d}{d x} f{\left(x \right)}$ :
  1. Rewrite the function to be differentiated:
    
    $\tan{\left(\sqrt{2 x} \right)} = \frac{\sin{\left(\sqrt{2 x} \right)}}{\cos{\left(\sqrt{2 x} \right)}}$
  2. Apply the quotient rule, which is:
    
    $\frac{d}{d x} \frac{f{\left(x \right)}}{g{\left(x \right)}} = \frac{- f{\left(x \right)} \frac{d}{d x} g{\left(x \right)} + g{\left(x \right)} \frac{d}{d x} f{\left(x \right)}}{g^{2}{\left(x \right)}}$
    
    $f{\left(x \right)} = \sin{\left(\sqrt{2 x} \right)}$ and $g{\left(x \right)} = \cos{\left(\sqrt{2 x} \right)}$ .
    
    To find $\frac{d}{d x} f{\left(x \right)}$ :
    1. Let $u = \sqrt{2 x}$ .
    2. The derivative of sine is cosine:
      
      $\frac{d}{d u} \sin{\left(u \right)} = \cos{\left(u \right)}$
    3. Then, apply the chain rule. Multiply by $\frac{d}{d x} \sqrt{2 x}$ :
      1. Let $u = 2 x$ .
      2. Apply the power rule: $\sqrt{u}$ goes to $\frac{1}{2 \sqrt{u}}$
      3. Then, apply the chain rule. Multiply by $\frac{d}{d x} 2 x$ :
        
        The derivative of a constant times a function is the constant times the derivative of the function.
        
        Apply the power rule: $x$ goes to $1$
        
        So, the result is: $2$
        
        The result of the chain rule is:
        
        $\frac{\sqrt{2}}{2 \sqrt{x}}$
      The result of the chain rule is:
      
      $\frac{\sqrt{2} \cos{\left(\sqrt{2 x} \right)}}{2 \sqrt{x}}$
    To find $\frac{d}{d x} g{\left(x \right)}$ :
    1. Let $u = \sqrt{2 x}$ .
    2. The derivative of cosine is negative sine:
      
      $\frac{d}{d u} \cos{\left(u \right)} = - \sin{\left(u \right)}$
    3. Then, apply the chain rule. Multiply by $\frac{d}{d x} \sqrt{2 x}$ :
      1. Let $u = 2 x$ .
      2. Apply the power rule: $\sqrt{u}$ goes to $\frac{1}{2 \sqrt{u}}$
      3. Then, apply the chain rule. Multiply by $\frac{d}{d x} 2 x$ :
        
        The derivative of a constant times a function is the constant times the derivative of the function.
        
        Apply the power rule: $x$ goes to $1$
        
        So, the result is: $2$
        
        The result of the chain rule is:
        
        $\frac{\sqrt{2}}{2 \sqrt{x}}$
      The result of the chain rule is:
      
      $- \frac{\sqrt{2} \sin{\left(\sqrt{2 x} \right)}}{2 \sqrt{x}}$
    Now plug in to the quotient rule:
    
    $\frac{\frac{\sqrt{2} \sin^{2}{\left(\sqrt{2 x} \right)}}{2 \sqrt{x}} + \frac{\sqrt{2} \cos^{2}{\left(\sqrt{2 x} \right)}}{2 \sqrt{x}}}{\cos^{2}{\left(\sqrt{2 x} \right)}}$
  To find $\frac{d}{d x} g{\left(x \right)}$ :
  1. Apply the power rule: $x$ goes to $1$
  Now plug in to the quotient rule:
  
  $\frac{\frac{x \left(\frac{\sqrt{2} \sin^{2}{\left(\sqrt{2 x} \right)}}{2 \sqrt{x}} + \frac{\sqrt{2} \cos^{2}{\left(\sqrt{2 x} \right)}}{2 \sqrt{x}}\right)}{\cos^{2}{\left(\sqrt{2 x} \right)}} - \tan{\left(\sqrt{2 x} \right)}}{x^{2}}$
2. The derivative of the constant $1$ is zero.
The result is: $\frac{\frac{x \left(\frac{\sqrt{2} \sin^{2}{\left(\sqrt{2 x} \right)}}{2 \sqrt{x}} + \frac{\sqrt{2} \cos^{2}{\left(\sqrt{2 x} \right)}}{2 \sqrt{x}}\right)}{\cos^{2}{\left(\sqrt{2 x} \right)}} - \tan{\left(\sqrt{2 x} \right)}}{x^{2}}$
Now simplify:

$\frac{\frac{\sqrt{2} \sqrt{x}}{2 \cos^{2}{\left(\sqrt{2} \sqrt{x} \right)}} - \tan{\left(\sqrt{2} \sqrt{x} \right)}}{x^{2}}$

The answer is:

$\frac{\frac{\sqrt{2} \sqrt{x}}{2 \cos^{2}{\left(\sqrt{2} \sqrt{x} \right)}} - \tan{\left(\sqrt{2} \sqrt{x} \right)}}{x^{2}}$

The graph

Plot the graph f(x)

Plot the graph f'(x)

The first derivative [src]

     /  _____\     ___ /       2/  _____\\
  tan\\/ 2*x /   \/ 2 *\1 + tan \\/ 2*x //
- ------------ + -------------------------
        2                     3/2         
       x                   2*x

$$- \frac{\tan{\left(\sqrt{2 x} \right)}}{x^{2}} + \frac{\sqrt{2} \left(\tan^{2}{\left(\sqrt{2 x} \right)} + 1\right)}{2 x^{\frac{3}{2}}}$$

Simplify

The second derivative [src]

     /  _____\   /       2/  _____\\    /  _____\       ___ /       2/  _____\\
2*tan\\/ 2*x /   \1 + tan \\/ 2*x //*tan\\/ 2*x /   5*\/ 2 *\1 + tan \\/ 2*x //
-------------- + -------------------------------- - ---------------------------
       3                         2                                5/2          
      x                         x                              4*x

$$\frac{\left(\tan^{2}{\left(\sqrt{2 x} \right)} + 1\right) \tan{\left(\sqrt{2 x} \right)}}{x^{2}} + \frac{2 \tan{\left(\sqrt{2 x} \right)}}{x^{3}} - \frac{5 \sqrt{2} \left(\tan^{2}{\left(\sqrt{2 x} \right)} + 1\right)}{4 x^{\frac{5}{2}}}$$

Simplify

3-я производная [src]

                                            2                                                                                                              
       /  _____\     ___ /       2/  _____\\      /       2/  _____\\    /  _____\        ___ /       2/  _____\\     ___    2/  _____\ /       2/  _____\\
  6*tan\\/ 2*x /   \/ 2 *\1 + tan \\/ 2*x //    9*\1 + tan \\/ 2*x //*tan\\/ 2*x /   33*\/ 2 *\1 + tan \\/ 2*x //   \/ 2 *tan \\/ 2*x /*\1 + tan \\/ 2*x //
- -------------- + -------------------------- - ---------------------------------- + ---------------------------- + ---------------------------------------
         4                      5/2                               3                                7/2                                 5/2                 
        x                    2*x                               2*x                              8*x                                   x

$$- \frac{9 \left(\tan^{2}{\left(\sqrt{2 x} \right)} + 1\right) \tan{\left(\sqrt{2 x} \right)}}{2 x^{3}} - \frac{6 \tan{\left(\sqrt{2 x} \right)}}{x^{4}} + \frac{\sqrt{2} \left(\tan^{2}{\left(\sqrt{2 x} \right)} + 1\right)^{2}}{2 x^{\frac{5}{2}}} + \frac{\sqrt{2} \left(\tan^{2}{\left(\sqrt{2 x} \right)} + 1\right) \tan^{2}{\left(\sqrt{2 x} \right)}}{x^{\frac{5}{2}}} + \frac{33 \sqrt{2} \left(\tan^{2}{\left(\sqrt{2 x} \right)} + 1\right)}{8 x^{\frac{7}{2}}}$$

Simplify

The third derivative [src]

                                            2                                                                                                              
       /  _____\     ___ /       2/  _____\\      /       2/  _____\\    /  _____\        ___ /       2/  _____\\     ___    2/  _____\ /       2/  _____\\
  6*tan\\/ 2*x /   \/ 2 *\1 + tan \\/ 2*x //    9*\1 + tan \\/ 2*x //*tan\\/ 2*x /   33*\/ 2 *\1 + tan \\/ 2*x //   \/ 2 *tan \\/ 2*x /*\1 + tan \\/ 2*x //
- -------------- + -------------------------- - ---------------------------------- + ---------------------------- + ---------------------------------------
         4                      5/2                               3                                7/2                                 5/2                 
        x                    2*x                               2*x                              8*x                                   x

Simplify

The graph

Other calculators

How to use it?

Identical expressions

Similar expressions

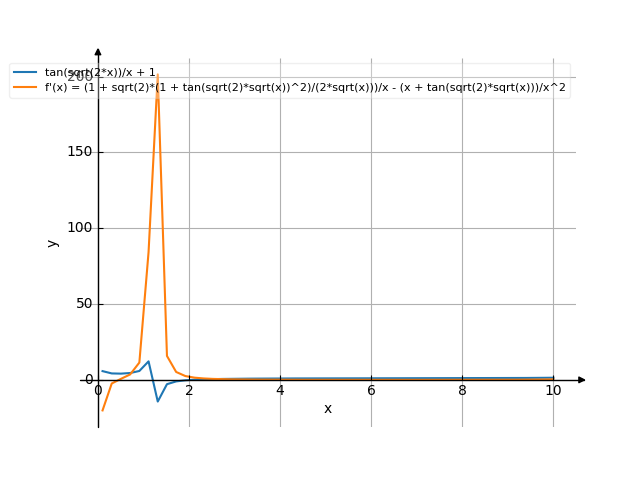
Derivative of y=tg√2x/x+1

The graph:

Piecewise:

The solution