Mister Exam
Other calculators
- Derivative of a implicit defined function
- Derivative of Parametric Function
- Partial derivative of the function
- Curve tracing functions Step by Step
- Integral Step by Step
- Differential equations Step by Step
- Limits Step by Step
-
How to use it?
- Derivative of:
-
Derivative of y=2x
-
Derivative of x^2/e^x
-
Derivative of (x-3)/(x+3)
-
Derivative of x^3/(2*x+4)
-
Identical expressions
- y=(sqrt(3x+ one))^sin5x
- y equally ( square root of (3x plus 1)) to the power of sinus of 5x
- y equally ( square root of (3x plus one)) to the power of sinus of 5x
- y=(√(3x+1))^sin5x
- y=(sqrt(3x+1))sin5x
- y=sqrt3x+1sin5x
- y=sqrt3x+1^sin5x
-
Similar expressions
- y=(sqrt(3x-1))^sin5x
Derivative of y=(sqrt(3x+1))^sin5x
The solution
You have entered
[src]
sin(5*x) _________ \/ 3*x + 1
$$\left(\sqrt{3 x + 1}\right)^{\sin{\left(5 x \right)}}$$
/ sin(5*x)\ d | _________ | --\\/ 3*x + 1 / dx
$$\frac{d}{d x} \left(\sqrt{3 x + 1}\right)^{\sin{\left(5 x \right)}}$$
Detail solution
-
Don't know the steps in finding this derivative.
But the derivative is
The answer is:
The first derivative
[src]
sin(5*x)
--------
2 / / _________\ 3*sin(5*x)\
(3*x + 1) *|5*cos(5*x)*log\\/ 3*x + 1 / + -----------|
\ 2*(3*x + 1)/
$$\left(3 x + 1\right)^{\frac{\sin{\left(5 x \right)}}{2}} \cdot \left(5 \log{\left(\sqrt{3 x + 1} \right)} \cos{\left(5 x \right)} + \frac{3 \sin{\left(5 x \right)}}{2 \cdot \left(3 x + 1\right)}\right)$$
The second derivative
[src]
sin(5*x) / /3*sin(5*x) \ /3*sin(5*x) / _________\\\
-------- | |---------- + 5*cos(5*x)*log(1 + 3*x)|*|---------- + 10*cos(5*x)*log\\/ 1 + 3*x /||
2 | / _________\ 15*cos(5*x) 9*sin(5*x) \ 1 + 3*x / \ 1 + 3*x /|
(1 + 3*x) *|- 25*log\\/ 1 + 3*x /*sin(5*x) + ----------- - ------------ + ----------------------------------------------------------------------------------|
| 1 + 3*x 2 4 |
\ 2*(1 + 3*x) /
$$\left(3 x + 1\right)^{\frac{\sin{\left(5 x \right)}}{2}} \left(\frac{\left(10 \log{\left(\sqrt{3 x + 1} \right)} \cos{\left(5 x \right)} + \frac{3 \sin{\left(5 x \right)}}{3 x + 1}\right) \left(5 \log{\left(3 x + 1 \right)} \cos{\left(5 x \right)} + \frac{3 \sin{\left(5 x \right)}}{3 x + 1}\right)}{4} - 25 \log{\left(\sqrt{3 x + 1} \right)} \sin{\left(5 x \right)} + \frac{15 \cos{\left(5 x \right)}}{3 x + 1} - \frac{9 \sin{\left(5 x \right)}}{2 \left(3 x + 1\right)^{2}}\right)$$
The third derivative
[src]
/ /3*sin(5*x) \ / 30*cos(5*x) 9*sin(5*x) / _________\ \ /3*sin(5*x) / _________\\ / 30*cos(5*x) 9*sin(5*x) \ 2 \
sin(5*x) | |---------- + 5*cos(5*x)*log(1 + 3*x)|*|- ----------- + ---------- + 50*log\\/ 1 + 3*x /*sin(5*x)| |---------- + 10*cos(5*x)*log\\/ 1 + 3*x /|*|- ----------- + ---------- + 25*log(1 + 3*x)*sin(5*x)| /3*sin(5*x) \ /3*sin(5*x) / _________\\|
-------- | \ 1 + 3*x / | 1 + 3*x 2 | \ 1 + 3*x / | 1 + 3*x 2 | |---------- + 5*cos(5*x)*log(1 + 3*x)| *|---------- + 10*cos(5*x)*log\\/ 1 + 3*x /||
2 | / _________\ 27*sin(5*x) 225*sin(5*x) 135*cos(5*x) \ (1 + 3*x) / \ (1 + 3*x) / \ 1 + 3*x / \ 1 + 3*x /|
(1 + 3*x) *|- 125*cos(5*x)*log\\/ 1 + 3*x / + ----------- - ------------ - ------------ - -------------------------------------------------------------------------------------------------- - --------------------------------------------------------------------------------------------------- + -----------------------------------------------------------------------------------|
| 3 2*(1 + 3*x) 2 2 4 8 |
\ (1 + 3*x) 2*(1 + 3*x) /
$$\left(3 x + 1\right)^{\frac{\sin{\left(5 x \right)}}{2}} \left(\frac{\left(10 \log{\left(\sqrt{3 x + 1} \right)} \cos{\left(5 x \right)} + \frac{3 \sin{\left(5 x \right)}}{3 x + 1}\right) \left(5 \log{\left(3 x + 1 \right)} \cos{\left(5 x \right)} + \frac{3 \sin{\left(5 x \right)}}{3 x + 1}\right)^{2}}{8} - \frac{\left(10 \log{\left(\sqrt{3 x + 1} \right)} \cos{\left(5 x \right)} + \frac{3 \sin{\left(5 x \right)}}{3 x + 1}\right) \left(25 \log{\left(3 x + 1 \right)} \sin{\left(5 x \right)} - \frac{30 \cos{\left(5 x \right)}}{3 x + 1} + \frac{9 \sin{\left(5 x \right)}}{\left(3 x + 1\right)^{2}}\right)}{4} - \frac{\left(5 \log{\left(3 x + 1 \right)} \cos{\left(5 x \right)} + \frac{3 \sin{\left(5 x \right)}}{3 x + 1}\right) \left(50 \log{\left(\sqrt{3 x + 1} \right)} \sin{\left(5 x \right)} - \frac{30 \cos{\left(5 x \right)}}{3 x + 1} + \frac{9 \sin{\left(5 x \right)}}{\left(3 x + 1\right)^{2}}\right)}{2} - 125 \log{\left(\sqrt{3 x + 1} \right)} \cos{\left(5 x \right)} - \frac{225 \sin{\left(5 x \right)}}{2 \cdot \left(3 x + 1\right)} - \frac{135 \cos{\left(5 x \right)}}{2 \left(3 x + 1\right)^{2}} + \frac{27 \sin{\left(5 x \right)}}{\left(3 x + 1\right)^{3}}\right)$$
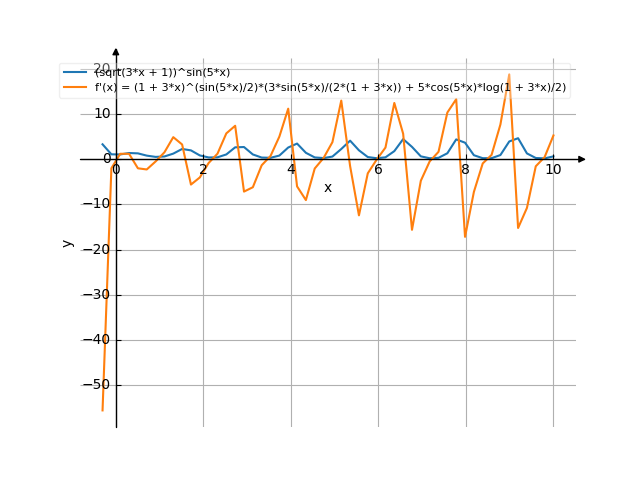
The graph