Mister Exam
Other calculators
- Derivative of a implicit defined function
- Derivative of Parametric Function
- Partial derivative of the function
- Curve tracing functions Step by Step
- Integral Step by Step
- Differential equations Step by Step
- Limits Step by Step
-
How to use it?
- Derivative of:
- Derivative of e^x^x
- Derivative of sqrt4
-
Derivative of cos(x)/e^x
-
Derivative of acos(1/x)
-
Identical expressions
- y=(ln5x)^sin(sqrt(4x- one))
- y equally (ln5x) to the power of sinus of ( square root of (4x minus 1))
- y equally (ln5x) to the power of sinus of ( square root of (4x minus one))
- y=(ln5x)^sin(√(4x-1))
- y=(ln5x)sin(sqrt(4x-1))
- y=ln5xsinsqrt4x-1
- y=ln5x^sinsqrt4x-1
-
Similar expressions
- y=(ln5x)^sin(sqrt(4x+1))
Derivative of y=(ln5x)^sin(sqrt(4x-1))
The solution
You have entered
[src]
/ _________\
sin\\/ 4*x - 1 /
(log(5*x))
$$\log{\left(5 x \right)}^{\sin{\left(\sqrt{4 x - 1} \right)}}$$
log(5*x)^sin(sqrt(4*x - 1))
Detail solution
-
Don't know the steps in finding this derivative.
But the derivative is
-
Now simplify:
The answer is:
The first derivative
[src]
/ _________\ / / _________\ / _________\ \
sin\\/ 4*x - 1 / |sin\\/ 4*x - 1 / 2*cos\\/ 4*x - 1 /*log(log(5*x))|
(log(5*x)) *|---------------- + --------------------------------|
| x*log(5*x) _________ |
\ \/ 4*x - 1 /
$$\left(\frac{2 \log{\left(\log{\left(5 x \right)} \right)} \cos{\left(\sqrt{4 x - 1} \right)}}{\sqrt{4 x - 1}} + \frac{\sin{\left(\sqrt{4 x - 1} \right)}}{x \log{\left(5 x \right)}}\right) \log{\left(5 x \right)}^{\sin{\left(\sqrt{4 x - 1} \right)}}$$
The second derivative
[src]
/ 2 \
/ __________\ |/ / __________\ / __________\ \ / __________\ / __________\ / __________\ / __________\ / __________\ |
sin\\/ -1 + 4*x / ||sin\\/ -1 + 4*x / 2*cos\\/ -1 + 4*x /*log(log(5*x))| sin\\/ -1 + 4*x / sin\\/ -1 + 4*x / 4*log(log(5*x))*sin\\/ -1 + 4*x / 4*cos\\/ -1 + 4*x /*log(log(5*x)) 4*cos\\/ -1 + 4*x / |
(log(5*x)) *||----------------- + ---------------------------------| - ----------------- - ----------------- - --------------------------------- - --------------------------------- + -----------------------|
|| x*log(5*x) __________ | 2 2 2 -1 + 4*x 3/2 __________ |
\\ \/ -1 + 4*x / x *log(5*x) x *log (5*x) (-1 + 4*x) x*\/ -1 + 4*x *log(5*x)/
$$\left(\left(\frac{2 \log{\left(\log{\left(5 x \right)} \right)} \cos{\left(\sqrt{4 x - 1} \right)}}{\sqrt{4 x - 1}} + \frac{\sin{\left(\sqrt{4 x - 1} \right)}}{x \log{\left(5 x \right)}}\right)^{2} - \frac{4 \log{\left(\log{\left(5 x \right)} \right)} \sin{\left(\sqrt{4 x - 1} \right)}}{4 x - 1} - \frac{4 \log{\left(\log{\left(5 x \right)} \right)} \cos{\left(\sqrt{4 x - 1} \right)}}{\left(4 x - 1\right)^{\frac{3}{2}}} + \frac{4 \cos{\left(\sqrt{4 x - 1} \right)}}{x \sqrt{4 x - 1} \log{\left(5 x \right)}} - \frac{\sin{\left(\sqrt{4 x - 1} \right)}}{x^{2} \log{\left(5 x \right)}} - \frac{\sin{\left(\sqrt{4 x - 1} \right)}}{x^{2} \log{\left(5 x \right)}^{2}}\right) \log{\left(5 x \right)}^{\sin{\left(\sqrt{4 x - 1} \right)}}$$
The third derivative
[src]
/ 3 \
/ __________\ |/ / __________\ / __________\ \ / / __________\ / __________\ \ / / __________\ / __________\ / __________\ / __________\ / __________\ \ / __________\ / __________\ / __________\ / __________\ / __________\ / __________\ / __________\ / __________\ / __________\ / __________\ |
sin\\/ -1 + 4*x / ||sin\\/ -1 + 4*x / 2*cos\\/ -1 + 4*x /*log(log(5*x))| |sin\\/ -1 + 4*x / 2*cos\\/ -1 + 4*x /*log(log(5*x))| |sin\\/ -1 + 4*x / sin\\/ -1 + 4*x / 4*log(log(5*x))*sin\\/ -1 + 4*x / 4*cos\\/ -1 + 4*x /*log(log(5*x)) 4*cos\\/ -1 + 4*x / | 8*cos\\/ -1 + 4*x /*log(log(5*x)) 2*sin\\/ -1 + 4*x / 2*sin\\/ -1 + 4*x / 3*sin\\/ -1 + 4*x / 24*log(log(5*x))*sin\\/ -1 + 4*x / 24*cos\\/ -1 + 4*x /*log(log(5*x)) 12*sin\\/ -1 + 4*x / 12*cos\\/ -1 + 4*x / 6*cos\\/ -1 + 4*x / 6*cos\\/ -1 + 4*x / |
(log(5*x)) *||----------------- + ---------------------------------| - 3*|----------------- + ---------------------------------|*|----------------- + ----------------- + --------------------------------- + --------------------------------- - -----------------------| - --------------------------------- + ------------------- + ------------------- + ------------------- + ---------------------------------- + ---------------------------------- - --------------------- - ------------------------ - ------------------------ - -------------------------|
|| x*log(5*x) __________ | | x*log(5*x) __________ | | 2 2 2 -1 + 4*x 3/2 __________ | 3/2 3 3 3 3 2 2 5/2 x*(-1 + 4*x)*log(5*x) 3/2 2 __________ 2 __________ 2 |
\\ \/ -1 + 4*x / \ \/ -1 + 4*x / \ x *log(5*x) x *log (5*x) (-1 + 4*x) x*\/ -1 + 4*x *log(5*x)/ (-1 + 4*x) x *log(5*x) x *log (5*x) x *log (5*x) (-1 + 4*x) (-1 + 4*x) x*(-1 + 4*x) *log(5*x) x *\/ -1 + 4*x *log(5*x) x *\/ -1 + 4*x *log (5*x)/
$$\left(\left(\frac{2 \log{\left(\log{\left(5 x \right)} \right)} \cos{\left(\sqrt{4 x - 1} \right)}}{\sqrt{4 x - 1}} + \frac{\sin{\left(\sqrt{4 x - 1} \right)}}{x \log{\left(5 x \right)}}\right)^{3} - 3 \left(\frac{2 \log{\left(\log{\left(5 x \right)} \right)} \cos{\left(\sqrt{4 x - 1} \right)}}{\sqrt{4 x - 1}} + \frac{\sin{\left(\sqrt{4 x - 1} \right)}}{x \log{\left(5 x \right)}}\right) \left(\frac{4 \log{\left(\log{\left(5 x \right)} \right)} \sin{\left(\sqrt{4 x - 1} \right)}}{4 x - 1} + \frac{4 \log{\left(\log{\left(5 x \right)} \right)} \cos{\left(\sqrt{4 x - 1} \right)}}{\left(4 x - 1\right)^{\frac{3}{2}}} - \frac{4 \cos{\left(\sqrt{4 x - 1} \right)}}{x \sqrt{4 x - 1} \log{\left(5 x \right)}} + \frac{\sin{\left(\sqrt{4 x - 1} \right)}}{x^{2} \log{\left(5 x \right)}} + \frac{\sin{\left(\sqrt{4 x - 1} \right)}}{x^{2} \log{\left(5 x \right)}^{2}}\right) + \frac{24 \log{\left(\log{\left(5 x \right)} \right)} \sin{\left(\sqrt{4 x - 1} \right)}}{\left(4 x - 1\right)^{2}} - \frac{8 \log{\left(\log{\left(5 x \right)} \right)} \cos{\left(\sqrt{4 x - 1} \right)}}{\left(4 x - 1\right)^{\frac{3}{2}}} + \frac{24 \log{\left(\log{\left(5 x \right)} \right)} \cos{\left(\sqrt{4 x - 1} \right)}}{\left(4 x - 1\right)^{\frac{5}{2}}} - \frac{12 \sin{\left(\sqrt{4 x - 1} \right)}}{x \left(4 x - 1\right) \log{\left(5 x \right)}} - \frac{12 \cos{\left(\sqrt{4 x - 1} \right)}}{x \left(4 x - 1\right)^{\frac{3}{2}} \log{\left(5 x \right)}} - \frac{6 \cos{\left(\sqrt{4 x - 1} \right)}}{x^{2} \sqrt{4 x - 1} \log{\left(5 x \right)}} - \frac{6 \cos{\left(\sqrt{4 x - 1} \right)}}{x^{2} \sqrt{4 x - 1} \log{\left(5 x \right)}^{2}} + \frac{2 \sin{\left(\sqrt{4 x - 1} \right)}}{x^{3} \log{\left(5 x \right)}} + \frac{3 \sin{\left(\sqrt{4 x - 1} \right)}}{x^{3} \log{\left(5 x \right)}^{2}} + \frac{2 \sin{\left(\sqrt{4 x - 1} \right)}}{x^{3} \log{\left(5 x \right)}^{3}}\right) \log{\left(5 x \right)}^{\sin{\left(\sqrt{4 x - 1} \right)}}$$
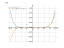
The graph