Derivative of x^4*atan(3x)
The solution
The second derivative
[src]
/ 3 \
2 | 9*x 4*x |
6*x *|2*atan(3*x) - ----------- + --------|
| 2 2|
| / 2\ 1 + 9*x |
\ \1 + 9*x / /

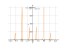 Derivative of sin(x)/cos(x)
Derivative of sin(x)/cos(x)
 Derivative of cos(x)^(3)
Derivative of cos(x)^(3)
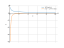 Derivative of 1/(2*sqrt(x))
Derivative of 1/(2*sqrt(x))
 Derivative of -x^4
Derivative of -x^4