Derivative of 2*3^x
The solution
Detail solution
-
The derivative of a constant times a function is the constant times the derivative of the function.
So, the result is:
The answer is:
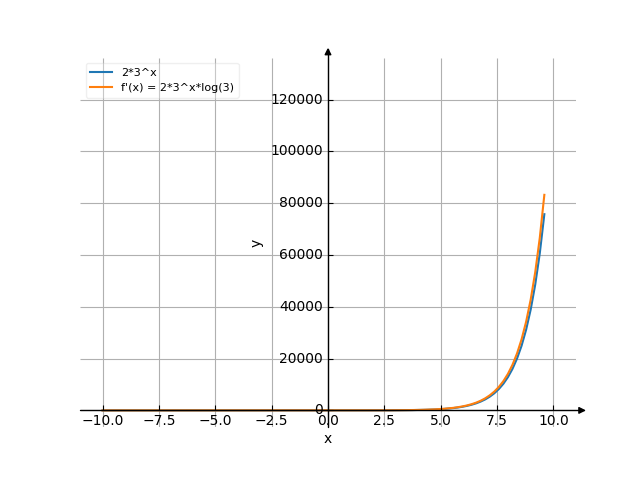
The graph
The derivative of a constant times a function is the constant times the derivative of the function.
So, the result is:
The answer is:
