Mister Exam

Other calculators

sqrt(1-3x^2)
The derivative of the function/ sqrt(1-3x^2)

Derivative of sqrt(1-3x^2)

Function f() - derivative -N order at the point
v

The graph:

from to

Piecewise:

The solution

You have entered [src] 
   __________
  /        2 
\/  1 - 3*x
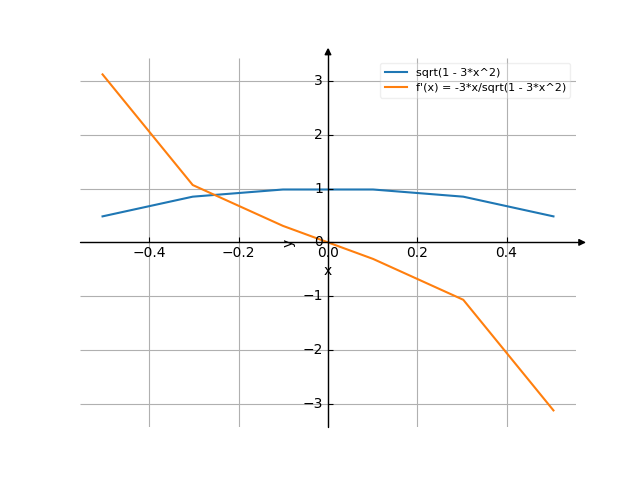
$$\sqrt{1 - 3 x^{2}}$$ 
  /   __________\
d |  /        2 |
--\\/  1 - 3*x  /
dx
$$\frac{d}{d x} \sqrt{1 - 3 x^{2}}$$
Transform
Detail solution

  1. Let .

  2. Apply the power rule: goes to

  3. Then, apply the chain rule. Multiply by :

    1. Differentiate term by term:

      1. The derivative of the constant is zero.

      2. The derivative of a constant times a function is the constant times the derivative of the function.

        1. The derivative of a constant times a function is the constant times the derivative of the function.

          1. Apply the power rule: goes to

          So, the result is:

        So, the result is:

      The result is:

    The result of the chain rule is:

  4. Now simplify:

The answer is:

The graph
Plot the graph f(x)
Plot the graph f'(x)
The first derivative [src] 
     -3*x    
-------------
   __________
  /        2 
\/  1 - 3*x
$$- \frac{3 x}{\sqrt{1 - 3 x^{2}}}$$
Simplify
The second derivative [src] 
   /         2  \
   |      3*x   |
-3*|1 + --------|
   |           2|
   \    1 - 3*x /
-----------------
     __________  
    /        2   
  \/  1 - 3*x
$$- \frac{3 \cdot \left(\frac{3 x^{2}}{1 - 3 x^{2}} + 1\right)}{\sqrt{1 - 3 x^{2}}}$$
Simplify
The third derivative [src] 
      /         2  \
      |      3*x   |
-27*x*|1 + --------|
      |           2|
      \    1 - 3*x /
--------------------
             3/2    
   /       2\       
   \1 - 3*x /
$$- \frac{27 x \left(\frac{3 x^{2}}{1 - 3 x^{2}} + 1\right)}{\left(1 - 3 x^{2}\right)^{\frac{3}{2}}}$$
Simplify
The graph
Derivative of sqrt(1-3x^2)
    © Mister Exam – Calculator