Derivative of sqrt(exp(-x)+8exp(3x^2))
The solution
_______________ / 2 / -x 3*x \/ e + 8*e
sqrt(exp(-x) + 8*exp(3*x^2))
-
Let .
-
Apply the power rule: goes to
-
Then, apply the chain rule. Multiply by :
-
Differentiate term by term:
-
Let .
-
The derivative of is itself.
-
-
Then, apply the chain rule. Multiply by :
-
The derivative of a constant times a function is the constant times the derivative of the function.
-
Apply the power rule: goes to
So, the result is:
-
The result of the chain rule is:
-
-
The derivative of a constant times a function is the constant times the derivative of the function.
-
Let .
-
The derivative of is itself.
-
-
Then, apply the chain rule. Multiply by :
-
The derivative of a constant times a function is the constant times the derivative of the function.
-
Apply the power rule: goes to
So, the result is:
-
The result of the chain rule is:
-
So, the result is:
-
The result is:
The result of the chain rule is:
Now simplify:
The answer is:
-x 2
e 3*x
- --- + 24*x*e
2
-------------------
_______________
/ 2
/ -x 3*x
\/ e + 8*e
2
/ 2\
-x 2 2 | -x 3*x |
e 3*x 2 3*x \- e + 48*x*e /
--- + 24*e + 144*x *e - ---------------------
2 / 2 \
| 3*x -x|
4*\8*e + e /
-----------------------------------------------------
_______________
/ 2
/ 3*x -x
\/ 8*e + e
3
/ 2\ / 2\ / 2 2 \
-x 2 2 | -x 3*x | | -x 3*x | | 3*x 2 3*x -x|
e 3*x 3 3*x 3*\- e + 48*x*e / 3*\- e + 48*x*e /*\48*e + 288*x *e + e /
- --- + 432*x*e + 864*x *e + ----------------------- - ------------------------------------------------------
2 2 / 2 \
/ 2 \ | 3*x -x|
| 3*x -x| 4*\8*e + e /
8*\8*e + e /
---------------------------------------------------------------------------------------------------------------------
_______________
/ 2
/ 3*x -x
\/ 8*e + e

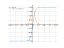 Derivative of tanh(x)
Derivative of tanh(x)
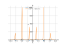 Derivative of tanx
Derivative of tanx
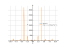 Derivative of tg2x
Derivative of tg2x
 Derivative of y=9
Derivative of y=9