Derivative of sin(x)^x
The solution
You have entered
[src]
x sin (x)
$$\sin^{x}{\left(x \right)}$$
d / x \ --\sin (x)/ dx
$$\frac{d}{d x} \sin^{x}{\left(x \right)}$$
Detail solution
-
Don't know the steps in finding this derivative.
But the derivative is
The answer is:
The first derivative
[src]
x /x*cos(x) \
sin (x)*|-------- + log(sin(x))|
\ sin(x) /
$$\left(\frac{x \cos{\left(x \right)}}{\sin{\left(x \right)}} + \log{\left(\sin{\left(x \right)} \right)}\right) \sin^{x}{\left(x \right)}$$
The second derivative
[src]
/ 2 2 \
x |/x*cos(x) \ 2*cos(x) x*cos (x)|
sin (x)*||-------- + log(sin(x))| - x + -------- - ---------|
|\ sin(x) / sin(x) 2 |
\ sin (x) /
$$\left(\left(\frac{x \cos{\left(x \right)}}{\sin{\left(x \right)}} + \log{\left(\sin{\left(x \right)} \right)}\right)^{2} - x - \frac{x \cos^{2}{\left(x \right)}}{\sin^{2}{\left(x \right)}} + \frac{2 \cos{\left(x \right)}}{\sin{\left(x \right)}}\right) \sin^{x}{\left(x \right)}$$
The third derivative
[src]
/ 3 2 / 2 \ 3 \
x | /x*cos(x) \ 3*cos (x) /x*cos(x) \ | 2*cos(x) x*cos (x)| 2*x*cos (x) 2*x*cos(x)|
sin (x)*|-3 + |-------- + log(sin(x))| - --------- - 3*|-------- + log(sin(x))|*|x - -------- + ---------| + ----------- + ----------|
| \ sin(x) / 2 \ sin(x) / | sin(x) 2 | 3 sin(x) |
\ sin (x) \ sin (x) / sin (x) /
$$\left(\left(\frac{x \cos{\left(x \right)}}{\sin{\left(x \right)}} + \log{\left(\sin{\left(x \right)} \right)}\right)^{3} - 3 \left(\frac{x \cos{\left(x \right)}}{\sin{\left(x \right)}} + \log{\left(\sin{\left(x \right)} \right)}\right) \left(x + \frac{x \cos^{2}{\left(x \right)}}{\sin^{2}{\left(x \right)}} - \frac{2 \cos{\left(x \right)}}{\sin{\left(x \right)}}\right) + \frac{2 x \cos{\left(x \right)}}{\sin{\left(x \right)}} + \frac{2 x \cos^{3}{\left(x \right)}}{\sin^{3}{\left(x \right)}} - 3 - \frac{3 \cos^{2}{\left(x \right)}}{\sin^{2}{\left(x \right)}}\right) \sin^{x}{\left(x \right)}$$
The graph
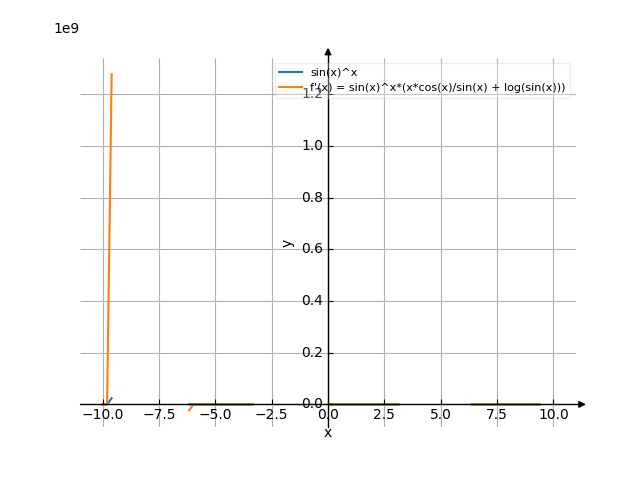

![Find the derivative of y' = f'(x) = sin(x)^x (sinus of (x) to the power of x) - functions. Find the derivative of the function at the point. [THERE'S THE ANSWER!] sin(x)^x](/media/krcore-image-pods/176/hash/derivative/3/30/c5b84263b624564598e11af06149b.png)
 Derivative of 4*x^2
Derivative of 4*x^2
 Derivative of 2^x^2
Derivative of 2^x^2
 Derivative of (x^2-1)/(x^2+1)
Derivative of (x^2-1)/(x^2+1)
 Derivative of x*e^(-x^2)
Derivative of x*e^(-x^2)
 sin(x)^x
sin(x)^x