Derivative of sinx/(5cosx+4)
The solution
You have entered
[src]
sin(x) ------------ 5*cos(x) + 4
$$\frac{\sin{\left(x \right)}}{5 \cos{\left(x \right)} + 4}$$
sin(x)/(5*cos(x) + 4)
Detail solution
-
Apply the quotient rule, which is:
and .
To find :
-
The derivative of sine is cosine:
To find :
-
Differentiate term by term:
-
The derivative of the constant is zero.
-
The derivative of a constant times a function is the constant times the derivative of the function.
-
The derivative of cosine is negative sine:
So, the result is:
-
The result is:
-
Now plug in to the quotient rule:
-
-
Now simplify:
The answer is:
The first derivative
[src]
2
cos(x) 5*sin (x)
------------ + ---------------
5*cos(x) + 4 2
(5*cos(x) + 4)
$$\frac{\cos{\left(x \right)}}{5 \cos{\left(x \right)} + 4} + \frac{5 \sin^{2}{\left(x \right)}}{\left(5 \cos{\left(x \right)} + 4\right)^{2}}$$
The second derivative
[src]
/ / 2 \ \
| | 10*sin (x) | |
| 5*|------------ + cos(x)| |
| \4 + 5*cos(x) / 10*cos(x) |
|-1 + ------------------------- + ------------|*sin(x)
\ 4 + 5*cos(x) 4 + 5*cos(x)/
------------------------------------------------------
4 + 5*cos(x)
$$\frac{\left(\frac{5 \left(\cos{\left(x \right)} + \frac{10 \sin^{2}{\left(x \right)}}{5 \cos{\left(x \right)} + 4}\right)}{5 \cos{\left(x \right)} + 4} - 1 + \frac{10 \cos{\left(x \right)}}{5 \cos{\left(x \right)} + 4}\right) \sin{\left(x \right)}}{5 \cos{\left(x \right)} + 4}$$
The third derivative
[src]
/ 2 \
2 | 30*cos(x) 150*sin (x) | / 2 \
5*sin (x)*|-1 + ------------ + ---------------| | 10*sin (x) |
2 | 4 + 5*cos(x) 2| 15*|------------ + cos(x)|*cos(x)
15*sin (x) \ (4 + 5*cos(x)) / \4 + 5*cos(x) /
-cos(x) - ------------ + ----------------------------------------------- + ---------------------------------
4 + 5*cos(x) 4 + 5*cos(x) 4 + 5*cos(x)
------------------------------------------------------------------------------------------------------------
4 + 5*cos(x)
$$\frac{\frac{15 \left(\cos{\left(x \right)} + \frac{10 \sin^{2}{\left(x \right)}}{5 \cos{\left(x \right)} + 4}\right) \cos{\left(x \right)}}{5 \cos{\left(x \right)} + 4} - \cos{\left(x \right)} + \frac{5 \left(-1 + \frac{30 \cos{\left(x \right)}}{5 \cos{\left(x \right)} + 4} + \frac{150 \sin^{2}{\left(x \right)}}{\left(5 \cos{\left(x \right)} + 4\right)^{2}}\right) \sin^{2}{\left(x \right)}}{5 \cos{\left(x \right)} + 4} - \frac{15 \sin^{2}{\left(x \right)}}{5 \cos{\left(x \right)} + 4}}{5 \cos{\left(x \right)} + 4}$$

 Derivative of 2*x^3-3*x^2+6*x+1
Derivative of 2*x^3-3*x^2+6*x+1
 Derivative of xarcsinx
Derivative of xarcsinx
 Derivative of x*cos(3*x)
Derivative of x*cos(3*x)
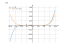 Derivative of x^7/10
Derivative of x^7/10