Mister Exam

Lang:

Other calculators

How to use it?
Derivative of:
Derivative of tan(x/2)-cot(x/2)
Derivative of log(x+3)
Derivative of sqrt4
Derivative of ln((x^2)/(1-x^2))
Identical expressions
(one +sqrt(x))/(one -sqrt(x))
(1 plus square root of (x)) divide by (1 minus square root of (x))
(one plus square root of (x)) divide by (one minus square root of (x))
(1+√(x))/(1-√(x))
1+sqrtx/1-sqrtx
(1+sqrt(x)) divide by (1-sqrt(x))
Similar expressions
(1-sqrt(x))/(1-sqrt(x))
(1+sqrtx)/(1-sqrtx)
1+sqrtx/(1-sqrt(x))
(1+sqrt(x))/(1+sqrt(x))

The derivative of the function/ (1+sqrt(x))/(1-sqrt(x))

Derivative of (1+sqrt(x))/(1-sqrt(x))

The solution

You have entered [src]

      ___
1 + \/ x 
---------
      ___
1 - \/ x

$$\frac{\sqrt{x} + 1}{1 - \sqrt{x}}$$

  /      ___\
d |1 + \/ x |
--|---------|
dx|      ___|
  \1 - \/ x /

$$\frac{d}{d x} \frac{\sqrt{x} + 1}{1 - \sqrt{x}}$$

Transform

Detail solution

Apply the quotient rule, which is:

$\frac{d}{d x} \frac{f{\left(x \right)}}{g{\left(x \right)}} = \frac{- f{\left(x \right)} \frac{d}{d x} g{\left(x \right)} + g{\left(x \right)} \frac{d}{d x} f{\left(x \right)}}{g^{2}{\left(x \right)}}$

$f{\left(x \right)} = \sqrt{x} + 1$ and $g{\left(x \right)} = 1 - \sqrt{x}$ .

To find $\frac{d}{d x} f{\left(x \right)}$ :
1. Differentiate $\sqrt{x} + 1$ term by term:
  1. The derivative of the constant $1$ is zero.
  2. Apply the power rule: $\sqrt{x}$ goes to $\frac{1}{2 \sqrt{x}}$
  The result is: $\frac{1}{2 \sqrt{x}}$
To find $\frac{d}{d x} g{\left(x \right)}$ :
1. Differentiate $1 - \sqrt{x}$ term by term:
  1. The derivative of the constant $1$ is zero.
  2. The derivative of a constant times a function is the constant times the derivative of the function.
    1. Apply the power rule: $\sqrt{x}$ goes to $\frac{1}{2 \sqrt{x}}$
    So, the result is: $- \frac{1}{2 \sqrt{x}}$
  The result is: $- \frac{1}{2 \sqrt{x}}$
Now plug in to the quotient rule:

$\frac{\frac{1 - \sqrt{x}}{2 \sqrt{x}} + \frac{\sqrt{x} + 1}{2 \sqrt{x}}}{\left(1 - \sqrt{x}\right)^{2}}$
Now simplify:

$\frac{1}{\sqrt{x} \left(\sqrt{x} - 1\right)^{2}}$

The answer is:

$\frac{1}{\sqrt{x} \left(\sqrt{x} - 1\right)^{2}}$

The graph

Plot the graph f(x)

Plot the graph f'(x)

The first derivative [src]

                                 ___      
         1                 1 + \/ x       
------------------- + --------------------
    ___ /      ___\                      2
2*\/ x *\1 - \/ x /       ___ /      ___\ 
                      2*\/ x *\1 - \/ x /

$$\frac{1}{2 \sqrt{x} \left(1 - \sqrt{x}\right)} + \frac{\sqrt{x} + 1}{2 \sqrt{x} \left(1 - \sqrt{x}\right)^{2}}$$

Simplify

The second derivative [src]

                        /      ___\ / 1           2       \
                        \1 + \/ x /*|---- + --------------|
                                    | 3/2     /       ___\|
 1           2                      \x      x*\-1 + \/ x //
---- + -------------- - -----------------------------------
 3/2     /       ___\                       ___            
x      x*\-1 + \/ x /                -1 + \/ x             
-----------------------------------------------------------
                         /       ___\                      
                       4*\-1 + \/ x /

$$\frac{- \frac{\left(\sqrt{x} + 1\right) \left(\frac{2}{x \left(\sqrt{x} - 1\right)} + \frac{1}{x^{\frac{3}{2}}}\right)}{\sqrt{x} - 1} + \frac{2}{x \left(\sqrt{x} - 1\right)} + \frac{1}{x^{\frac{3}{2}}}}{4 \left(\sqrt{x} - 1\right)}$$

Simplify

The third derivative [src]

  /                           /      ___\ / 1            2                  2         \                        \
  |                           \1 + \/ x /*|---- + --------------- + ------------------|    1           2       |
  |                                       | 5/2    2 /       ___\                    2|   ---- + --------------|
  |                                       |x      x *\-1 + \/ x /    3/2 /       ___\ |    3/2     /       ___\|
  |   1            1                      \                         x   *\-1 + \/ x / /   x      x*\-1 + \/ x /|
3*|- ---- - --------------- + --------------------------------------------------------- - ---------------------|
  |   5/2    2 /       ___\                                  ___                              ___ /       ___\ |
  \  x      x *\-1 + \/ x /                           -1 + \/ x                             \/ x *\-1 + \/ x / /
----------------------------------------------------------------------------------------------------------------
                                                   /       ___\                                                 
                                                 8*\-1 + \/ x /

$$\frac{3 \left(\frac{\left(\sqrt{x} + 1\right) \left(\frac{2}{x^{2} \left(\sqrt{x} - 1\right)} + \frac{2}{x^{\frac{3}{2}} \left(\sqrt{x} - 1\right)^{2}} + \frac{1}{x^{\frac{5}{2}}}\right)}{\sqrt{x} - 1} - \frac{1}{x^{2} \left(\sqrt{x} - 1\right)} - \frac{\frac{2}{x \left(\sqrt{x} - 1\right)} + \frac{1}{x^{\frac{3}{2}}}}{\sqrt{x} \left(\sqrt{x} - 1\right)} - \frac{1}{x^{\frac{5}{2}}}\right)}{8 \left(\sqrt{x} - 1\right)}$$

Simplify

The graph

Other calculators

How to use it?

Identical expressions

Similar expressions

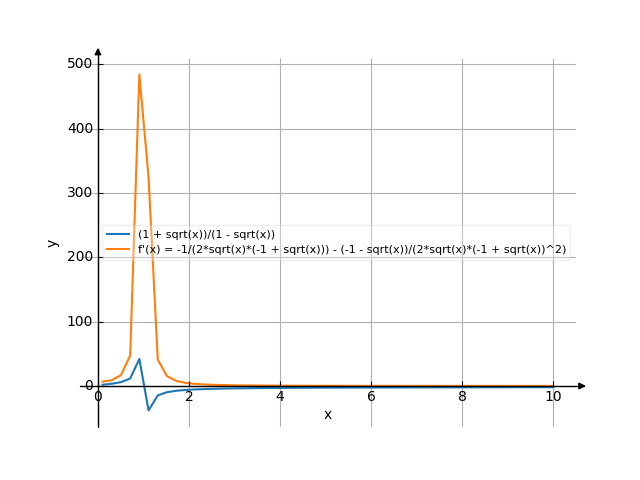
Derivative of (1+sqrt(x))/(1-sqrt(x))

The graph:

Piecewise:

The solution