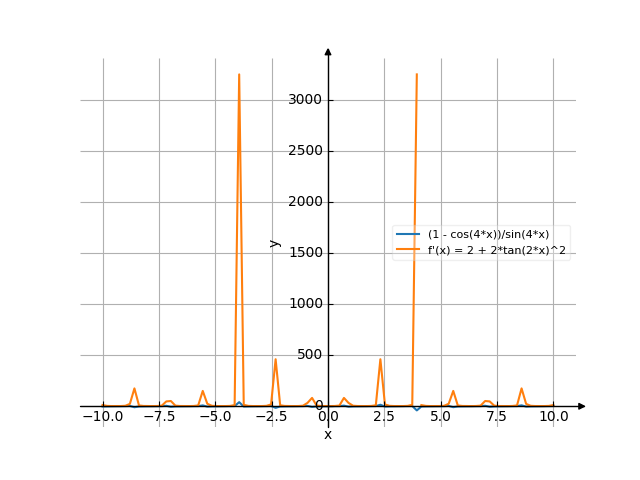
Türev (1-cos4x)/sin4x
Çözüm
1 - cos(4*x) ------------ sin(4*x)
d /1 - cos(4*x)\ --|------------| dx\ sin(4*x) /
-
Apply the quotient rule, which is:
and .
To find :
-
Differentiate term by term:
-
The derivative of the constant is zero.
-
The derivative of a constant times a function is the constant times the derivative of the function.
-
Let .
-
The derivative of cosine is negative sine:
-
-
Then, apply the chain rule. Multiply by :
-
The derivative of a constant times a function is the constant times the derivative of the function.
-
Apply the power rule: goes to
So, the result is:
-
The result of the chain rule is:
-
So, the result is:
-
The result is:
-
To find :
-
Let .
-
The derivative of sine is cosine:
-
Then, apply the chain rule. Multiply by :
-
The derivative of a constant times a function is the constant times the derivative of the function.
-
Apply the power rule: goes to
So, the result is:
-
The result of the chain rule is:
-
Now plug in to the quotient rule:
Now simplify:
The answer is:
4*(1 - cos(4*x))*cos(4*x)
4 - -------------------------
2
sin (4*x)
// 2 \ \
|| 2*cos (4*x)| |
-16*||1 + -----------|*(-1 + cos(4*x)) + cos(4*x)|
|| 2 | |
\\ sin (4*x) / /
--------------------------------------------------
sin(4*x)
/ / 2 \ \ | | 6*cos (4*x)| | | (-1 + cos(4*x))*|5 + -----------|*cos(4*x)| | 2 | 2 | | | 3*cos (4*x) \ sin (4*x) / | 64*|2 + ----------- + ------------------------------------------| | 2 2 | \ sin (4*x) sin (4*x) /

![Türevi bulun y' = f'(x) = (1-cos4x)/sin4x ((1 eksi ko sinüsü üsü 4x) böl sinüsü 4x) - Fonksiyon. Fonksiyonun türevinin değerini bir noktada bulalım. [CEVAP VAR!] (1-cos4x)/sin4x](/media/krcore-image-pods/176/hash/derivative/b/6a/8cc3d1ebf1f39e7c833659ea0b5c2.png)
 Türev (1-cos4x)/sin4x
Türev (1-cos4x)/sin4x
 Türev ze^z
Türev ze^z
 Türev x/sqrt(1-x^2)
Türev x/sqrt(1-x^2)
 Türev f(x)=4x²-5x³+9x
Türev f(x)=4x²-5x³+9x