Mister Exam

Other calculators

The derivative of the function/ |x|/(x^2+1)

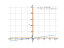
Derivative of |x|/(x^2+1)

Function f() - derivative -N order at the point
v

The graph:

from to

Piecewise:

The solution

You have entered [src] 
 |x|  
------
 2    
x  + 1
$$\frac{\left|{x}\right|}{x^{2} + 1}$$ 
|x|/(x^2 + 1)
The first derivative [src] 
sign(x)    2*x*|x| 
------- - ---------
  2               2
 x  + 1   / 2    \ 
          \x  + 1/
$$- \frac{2 x \left|{x}\right|}{\left(x^{2} + 1\right)^{2}} + \frac{\operatorname{sign}{\left(x \right)}}{x^{2} + 1}$$
Simplify
The second derivative [src] 
  //         2 \                                  \
  ||      4*x  |                                  |
  ||-1 + ------|*|x|                              |
  ||          2|                                  |
  |\     1 + x /       2*x*sign(x)                |
2*|----------------- - ----------- + DiracDelta(x)|
  |           2                2                  |
  \      1 + x            1 + x                   /
---------------------------------------------------
                            2                      
                       1 + x
$$\frac{2 \left(- \frac{2 x \operatorname{sign}{\left(x \right)}}{x^{2} + 1} + \delta\left(x\right) + \frac{\left(\frac{4 x^{2}}{x^{2} + 1} - 1\right) \left|{x}\right|}{x^{2} + 1}\right)}{x^{2} + 1}$$
Simplify
The third derivative [src] 
  /                        /         2 \                /         2 \                       \
  |                        |      4*x  |                |      2*x  |                       |
  |                      3*|-1 + ------|*sign(x)   12*x*|-1 + ------|*|x|                   |
  |                        |          2|                |          2|                       |
  |  6*x*DiracDelta(x)     \     1 + x /                \     1 + x /                       |
2*|- ----------------- + ----------------------- - ---------------------- + DiracDelta(x, 1)|
  |             2                      2                         2                          |
  |        1 + x                  1 + x                  /     2\                           |
  \                                                      \1 + x /                           /
---------------------------------------------------------------------------------------------
                                                 2                                           
                                            1 + x
$$\frac{2 \left(- \frac{6 x \delta\left(x\right)}{x^{2} + 1} - \frac{12 x \left(\frac{2 x^{2}}{x^{2} + 1} - 1\right) \left|{x}\right|}{\left(x^{2} + 1\right)^{2}} + \delta^{\left( 1 \right)}\left( x \right) + \frac{3 \left(\frac{4 x^{2}}{x^{2} + 1} - 1\right) \operatorname{sign}{\left(x \right)}}{x^{2} + 1}\right)}{x^{2} + 1}$$
Simplify
    © Mister Exam – Calculator