Mister Exam

Other calculators

-(((ctgx)^3)/3)
The derivative of the function/ -(((ctgx)^3)/3)

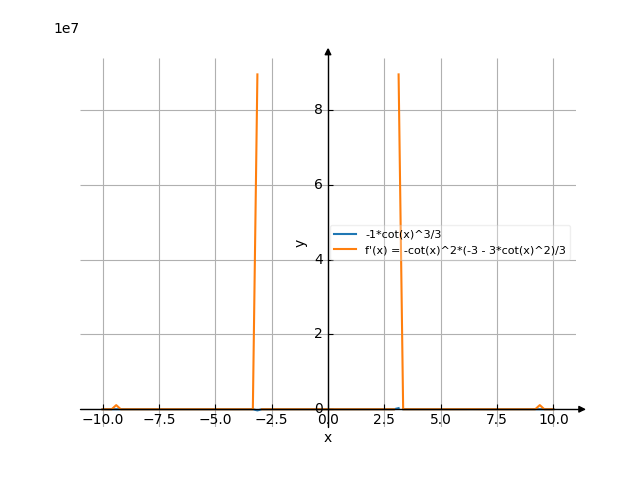
Derivative of -(((ctgx)^3)/3)

Function f() - derivative -N order at the point
v

The graph:

from to

Piecewise:

The solution

You have entered [src] 
    3    
-cot (x) 
---------
    3
−cot⁡3(x)3- \frac{\cot^{3}{\left(x \right)}}{3} 
  /    3    \
d |-cot (x) |
--|---------|
dx\    3    /
ddx(−cot⁡3(x)3)\frac{d}{d x} \left(- \frac{\cot^{3}{\left(x \right)}}{3}\right)
Transform
Detail solution

  1. The derivative of a constant times a function is the constant times the derivative of the function.

    1. Let u=cot⁡(x)u = \cot{\left(x \right)}.

    2. Apply the power rule: u3u^{3} goes to 3u23 u^{2}

    3. Then, apply the chain rule. Multiply by ddxcot⁡(x)\frac{d}{d x} \cot{\left(x \right)}:

      1. There are multiple ways to do this derivative.

        Method #1

        1. Rewrite the function to be differentiated:

          cot⁡(x)=1tan⁡(x)\cot{\left(x \right)} = \frac{1}{\tan{\left(x \right)}}

        2. Let u=tan⁡(x)u = \tan{\left(x \right)}.

        3. Apply the power rule: 1u\frac{1}{u} goes to −1u2- \frac{1}{u^{2}}

        4. Then, apply the chain rule. Multiply by ddxtan⁡(x)\frac{d}{d x} \tan{\left(x \right)}:

          1. Rewrite the function to be differentiated:

            tan⁡(x)=sin⁡(x)cos⁡(x)\tan{\left(x \right)} = \frac{\sin{\left(x \right)}}{\cos{\left(x \right)}}

          2. Apply the quotient rule, which is:

            ddxf(x)g(x)=−f(x)ddxg(x)+g(x)ddxf(x)g2(x)\frac{d}{d x} \frac{f{\left(x \right)}}{g{\left(x \right)}} = \frac{- f{\left(x \right)} \frac{d}{d x} g{\left(x \right)} + g{\left(x \right)} \frac{d}{d x} f{\left(x \right)}}{g^{2}{\left(x \right)}}

            f(x)=sin⁡(x)f{\left(x \right)} = \sin{\left(x \right)} and g(x)=cos⁡(x)g{\left(x \right)} = \cos{\left(x \right)}.

            To find ddxf(x)\frac{d}{d x} f{\left(x \right)}:

            1. The derivative of sine is cosine:

              ddxsin⁡(x)=cos⁡(x)\frac{d}{d x} \sin{\left(x \right)} = \cos{\left(x \right)}

            To find ddxg(x)\frac{d}{d x} g{\left(x \right)}:

            1. The derivative of cosine is negative sine:

              ddxcos⁡(x)=−sin⁡(x)\frac{d}{d x} \cos{\left(x \right)} = - \sin{\left(x \right)}

            Now plug in to the quotient rule:

            sin⁡2(x)+cos⁡2(x)cos⁡2(x)\frac{\sin^{2}{\left(x \right)} + \cos^{2}{\left(x \right)}}{\cos^{2}{\left(x \right)}}

          The result of the chain rule is:

          −sin⁡2(x)+cos⁡2(x)cos⁡2(x)tan⁡2(x)- \frac{\sin^{2}{\left(x \right)} + \cos^{2}{\left(x \right)}}{\cos^{2}{\left(x \right)} \tan^{2}{\left(x \right)}}

        Method #2

        1. Rewrite the function to be differentiated:

          cot⁡(x)=cos⁡(x)sin⁡(x)\cot{\left(x \right)} = \frac{\cos{\left(x \right)}}{\sin{\left(x \right)}}

        2. Apply the quotient rule, which is:

          ddxf(x)g(x)=−f(x)ddxg(x)+g(x)ddxf(x)g2(x)\frac{d}{d x} \frac{f{\left(x \right)}}{g{\left(x \right)}} = \frac{- f{\left(x \right)} \frac{d}{d x} g{\left(x \right)} + g{\left(x \right)} \frac{d}{d x} f{\left(x \right)}}{g^{2}{\left(x \right)}}

          f(x)=cos⁡(x)f{\left(x \right)} = \cos{\left(x \right)} and g(x)=sin⁡(x)g{\left(x \right)} = \sin{\left(x \right)}.

          To find ddxf(x)\frac{d}{d x} f{\left(x \right)}:

          1. The derivative of cosine is negative sine:

            ddxcos⁡(x)=−sin⁡(x)\frac{d}{d x} \cos{\left(x \right)} = - \sin{\left(x \right)}

          To find ddxg(x)\frac{d}{d x} g{\left(x \right)}:

          1. The derivative of sine is cosine:

            ddxsin⁡(x)=cos⁡(x)\frac{d}{d x} \sin{\left(x \right)} = \cos{\left(x \right)}

          Now plug in to the quotient rule:

          −sin⁡2(x)−cos⁡2(x)sin⁡2(x)\frac{- \sin^{2}{\left(x \right)} - \cos^{2}{\left(x \right)}}{\sin^{2}{\left(x \right)}}

      The result of the chain rule is:

      −3(sin⁡2(x)+cos⁡2(x))cot⁡2(x)cos⁡2(x)tan⁡2(x)- \frac{3 \left(\sin^{2}{\left(x \right)} + \cos^{2}{\left(x \right)}\right) \cot^{2}{\left(x \right)}}{\cos^{2}{\left(x \right)} \tan^{2}{\left(x \right)}}

    So, the result is: (sin⁡2(x)+cos⁡2(x))cot⁡2(x)cos⁡2(x)tan⁡2(x)\frac{\left(\sin^{2}{\left(x \right)} + \cos^{2}{\left(x \right)}\right) \cot^{2}{\left(x \right)}}{\cos^{2}{\left(x \right)} \tan^{2}{\left(x \right)}}

  2. Now simplify:

    cos⁡2(x)sin⁡4(x)\frac{\cos^{2}{\left(x \right)}}{\sin^{4}{\left(x \right)}}

The answer is:

cos⁡2(x)sin⁡4(x)\frac{\cos^{2}{\left(x \right)}}{\sin^{4}{\left(x \right)}}

The graph
02468-8-6-4-2-1010-100000000100000000
Plot the graph f(x)
Plot the graph f'(x)
The first derivative [src] 
    2    /          2   \ 
-cot (x)*\-3 - 3*cot (x)/ 
--------------------------
            3
−(−3cot⁡2(x)−3)cot⁡2(x)3- \frac{\left(- 3 \cot^{2}{\left(x \right)} - 3\right) \cot^{2}{\left(x \right)}}{3}
Simplify
The second derivative [src] 
   /       2   \ /         2   \       
-2*\1 + cot (x)/*\1 + 2*cot (x)/*cot(x)
−2(cot⁡2(x)+1)(2cot⁡2(x)+1)cot⁡(x)- 2 \left(\cot^{2}{\left(x \right)} + 1\right) \left(2 \cot^{2}{\left(x \right)} + 1\right) \cot{\left(x \right)}
Simplify
The third derivative [src] 
                /             2                                      \
  /       2   \ |/       2   \         4           2    /       2   \|
2*\1 + cot (x)/*\\1 + cot (x)/  + 2*cot (x) + 7*cot (x)*\1 + cot (x)//
2(cot⁡2(x)+1)((cot⁡2(x)+1)2+7(cot⁡2(x)+1)cot⁡2(x)+2cot⁡4(x))2 \left(\cot^{2}{\left(x \right)} + 1\right) \left(\left(\cot^{2}{\left(x \right)} + 1\right)^{2} + 7 \left(\cot^{2}{\left(x \right)} + 1\right) \cot^{2}{\left(x \right)} + 2 \cot^{4}{\left(x \right)}\right)
Simplify
The graph
Derivative of -(((ctgx)^3)/3)
    © Mister Exam – Calculator