Derivative of ln(tg3x+x^3)

The solution

You have entered [src]

   /            3\
log\tan(3*x) + x /

$$\log{\left(x^{3} + \tan{\left(3 x \right)} \right)}$$

d /   /            3\\
--\log\tan(3*x) + x //
dx

$$\frac{d}{d x} \log{\left(x^{3} + \tan{\left(3 x \right)} \right)}$$

Transform

Detail solution

Let $u = x^{3} + \tan{\left(3 x \right)}$ .
The derivative of $\log{\left(u \right)}$ is $\frac{1}{u}$ .
Then, apply the chain rule. Multiply by $\frac{d}{d x} \left(x^{3} + \tan{\left(3 x \right)}\right)$ :
1. Differentiate $x^{3} + \tan{\left(3 x \right)}$ term by term:
  1. Rewrite the function to be differentiated:
    
    $\tan{\left(3 x \right)} = \frac{\sin{\left(3 x \right)}}{\cos{\left(3 x \right)}}$
  2. Apply the quotient rule, which is:
    
    $\frac{d}{d x} \frac{f{\left(x \right)}}{g{\left(x \right)}} = \frac{- f{\left(x \right)} \frac{d}{d x} g{\left(x \right)} + g{\left(x \right)} \frac{d}{d x} f{\left(x \right)}}{g^{2}{\left(x \right)}}$
    
    $f{\left(x \right)} = \sin{\left(3 x \right)}$ and $g{\left(x \right)} = \cos{\left(3 x \right)}$ .
    
    To find $\frac{d}{d x} f{\left(x \right)}$ :
    1. Let $u = 3 x$ .
    2. The derivative of sine is cosine:
      
      $\frac{d}{d u} \sin{\left(u \right)} = \cos{\left(u \right)}$
    3. Then, apply the chain rule. Multiply by $\frac{d}{d x} 3 x$ :
      1. The derivative of a constant times a function is the constant times the derivative of the function.
        
        Apply the power rule: $x$ goes to $1$
        
        So, the result is: $3$
      The result of the chain rule is:
      
      $3 \cos{\left(3 x \right)}$
    To find $\frac{d}{d x} g{\left(x \right)}$ :
    1. Let $u = 3 x$ .
    2. The derivative of cosine is negative sine:
      
      $\frac{d}{d u} \cos{\left(u \right)} = - \sin{\left(u \right)}$
    3. Then, apply the chain rule. Multiply by $\frac{d}{d x} 3 x$ :
      1. The derivative of a constant times a function is the constant times the derivative of the function.
        
        Apply the power rule: $x$ goes to $1$
        
        So, the result is: $3$
      The result of the chain rule is:
      
      $- 3 \sin{\left(3 x \right)}$
    Now plug in to the quotient rule:
    
    $\frac{3 \sin^{2}{\left(3 x \right)} + 3 \cos^{2}{\left(3 x \right)}}{\cos^{2}{\left(3 x \right)}}$
  3. Apply the power rule: $x^{3}$ goes to $3 x^{2}$
  The result is: $3 x^{2} + \frac{3 \sin^{2}{\left(3 x \right)} + 3 \cos^{2}{\left(3 x \right)}}{\cos^{2}{\left(3 x \right)}}$
The result of the chain rule is:

$\frac{3 x^{2} + \frac{3 \sin^{2}{\left(3 x \right)} + 3 \cos^{2}{\left(3 x \right)}}{\cos^{2}{\left(3 x \right)}}}{x^{3} + \tan{\left(3 x \right)}}$
Now simplify:

$\frac{3 \left(x^{2} \cos^{2}{\left(3 x \right)} + 1\right)}{\left(x^{3} + \tan{\left(3 x \right)}\right) \cos^{2}{\left(3 x \right)}}$

The answer is:

$\frac{3 \left(x^{2} \cos^{2}{\left(3 x \right)} + 1\right)}{\left(x^{3} + \tan{\left(3 x \right)}\right) \cos^{2}{\left(3 x \right)}}$

The graph

Plot the graph f(x)

Plot the graph f'(x)

The first derivative [src]

       2        2     
3 + 3*x  + 3*tan (3*x)
----------------------
                3     
    tan(3*x) + x

$$\frac{3 x^{2} + 3 \tan^{2}{\left(3 x \right)} + 3}{x^{3} + \tan{\left(3 x \right)}}$$

Simplify

The second derivative [src]

  /                            2                             \
  |        /     2      2     \                              |
  |      3*\1 + x  + tan (3*x)/      /       2     \         |
3*|2*x - ----------------------- + 6*\1 + tan (3*x)/*tan(3*x)|
  |            3                                             |
  \           x  + tan(3*x)                                  /
--------------------------------------------------------------
                         3                                    
                        x  + tan(3*x)

$$\frac{3 \cdot \left(2 x + 6 \left(\tan^{2}{\left(3 x \right)} + 1\right) \tan{\left(3 x \right)} - \frac{3 \left(x^{2} + \tan^{2}{\left(3 x \right)} + 1\right)^{2}}{x^{3} + \tan{\left(3 x \right)}}\right)}{x^{3} + \tan{\left(3 x \right)}}$$

Simplify

The third derivative [src]

  /                                               3                                                                                         \
  |                     2     /     2      2     \                                     /      /       2     \         \ /     2      2     \|
  |      /       2     \    9*\1 + x  + tan (3*x)/          2      /       2     \   9*\x + 3*\1 + tan (3*x)/*tan(3*x)/*\1 + x  + tan (3*x)/|
6*|1 + 9*\1 + tan (3*x)/  + ----------------------- + 18*tan (3*x)*\1 + tan (3*x)/ - -------------------------------------------------------|
  |                                            2                                                           3                                |
  |                             / 3           \                                                           x  + tan(3*x)                     |
  \                             \x  + tan(3*x)/                                                                                             /
---------------------------------------------------------------------------------------------------------------------------------------------
                                                                 3                                                                           
                                                                x  + tan(3*x)

$$\frac{6 \left(- \frac{9 \left(x + 3 \left(\tan^{2}{\left(3 x \right)} + 1\right) \tan{\left(3 x \right)}\right) \left(x^{2} + \tan^{2}{\left(3 x \right)} + 1\right)}{x^{3} + \tan{\left(3 x \right)}} + 9 \left(\tan^{2}{\left(3 x \right)} + 1\right)^{2} + 18 \left(\tan^{2}{\left(3 x \right)} + 1\right) \tan^{2}{\left(3 x \right)} + 1 + \frac{9 \left(x^{2} + \tan^{2}{\left(3 x \right)} + 1\right)^{3}}{\left(x^{3} + \tan{\left(3 x \right)}\right)^{2}}\right)}{x^{3} + \tan{\left(3 x \right)}}$$

Simplify

The graph

Other calculators

How to use it?

Identical expressions

Similar expressions

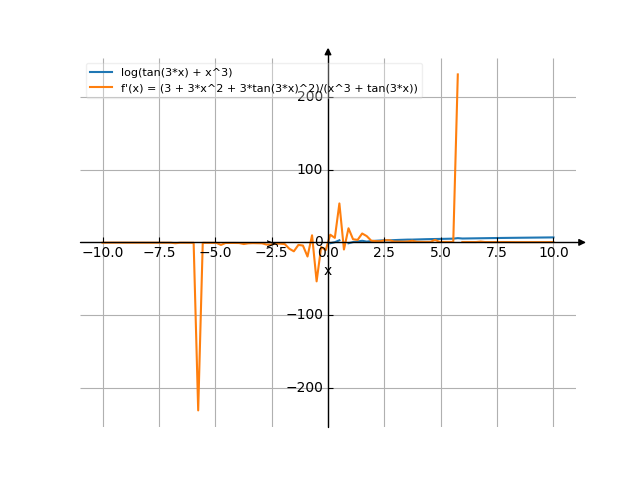
Derivative of ln(tg3x+x^3)

The graph:

Piecewise:

The solution