Mister Exam

Lang:

Other calculators

How to use it?
Derivative of:
Derivative of x^(-2)
Derivative of (x^2-1)^3
Derivative of sqrt(1/x)
Derivative of sin(x)^(9)
Identical expressions
ln(sin(5x)^ four)^ three
ln( sinus of (5x) to the power of 4) cubed
ln( sinus of (5x) to the power of four) to the power of three
ln(sin(5x)4)3
lnsin5x43
ln(sin(5x)⁴)³
ln(sin(5x) to the power of 4) to the power of 3
lnsin5x^4^3

The derivative of the function/ ln(sin(5x)^4)^3

Derivative of ln(sin(5x)^4)^3

The solution

You have entered [src]

   3/   4     \
log \sin (5*x)/

$$\log{\left(\sin^{4}{\left(5 x \right)} \right)}^{3}$$

d /   3/   4     \\
--\log \sin (5*x)//
dx

$$\frac{d}{d x} \log{\left(\sin^{4}{\left(5 x \right)} \right)}^{3}$$

Transform

Detail solution

Let $u = \log{\left(\sin^{4}{\left(5 x \right)} \right)}$ .
Apply the power rule: $u^{3}$ goes to $3 u^{2}$
Then, apply the chain rule. Multiply by $\frac{d}{d x} \log{\left(\sin^{4}{\left(5 x \right)} \right)}$ :
1. Let $u = \sin^{4}{\left(5 x \right)}$ .
2. The derivative of $\log{\left(u \right)}$ is $\frac{1}{u}$ .
3. Then, apply the chain rule. Multiply by $\frac{d}{d x} \sin^{4}{\left(5 x \right)}$ :
  1. Let $u = \sin{\left(5 x \right)}$ .
  2. Apply the power rule: $u^{4}$ goes to $4 u^{3}$
  3. Then, apply the chain rule. Multiply by $\frac{d}{d x} \sin{\left(5 x \right)}$ :
    1. Let $u = 5 x$ .
    2. The derivative of sine is cosine:
      
      $\frac{d}{d u} \sin{\left(u \right)} = \cos{\left(u \right)}$
    3. Then, apply the chain rule. Multiply by $\frac{d}{d x} 5 x$ :
      1. The derivative of a constant times a function is the constant times the derivative of the function.
        
        Apply the power rule: $x$ goes to $1$
        
        So, the result is: $5$
      The result of the chain rule is:
      
      $5 \cos{\left(5 x \right)}$
    The result of the chain rule is:
    
    $20 \sin^{3}{\left(5 x \right)} \cos{\left(5 x \right)}$
  The result of the chain rule is:
  
  $\frac{20 \cos{\left(5 x \right)}}{\sin{\left(5 x \right)}}$
The result of the chain rule is:

$\frac{60 \log{\left(\sin^{4}{\left(5 x \right)} \right)}^{2} \cos{\left(5 x \right)}}{\sin{\left(5 x \right)}}$
Now simplify:

$\frac{60 \log{\left(\sin^{4}{\left(5 x \right)} \right)}^{2}}{\tan{\left(5 x \right)}}$

The answer is:

$\frac{60 \log{\left(\sin^{4}{\left(5 x \right)} \right)}^{2}}{\tan{\left(5 x \right)}}$

The graph

Plot the graph f(x)

Plot the graph f'(x)

The first derivative [src]

      2/   4     \         
60*log \sin (5*x)/*cos(5*x)
---------------------------
          sin(5*x)

$$\frac{60 \log{\left(\sin^{4}{\left(5 x \right)} \right)}^{2} \cos{\left(5 x \right)}}{\sin{\left(5 x \right)}}$$

Simplify

The second derivative [src]

    /                        2           2         /   4     \\               
    |     /   4     \   8*cos (5*x)   cos (5*x)*log\sin (5*x)/|    /   4     \
300*|- log\sin (5*x)/ + ----------- - ------------------------|*log\sin (5*x)/
    |                       2                   2             |               
    \                    sin (5*x)           sin (5*x)        /

$$300 \left(- \log{\left(\sin^{4}{\left(5 x \right)} \right)} - \frac{\log{\left(\sin^{4}{\left(5 x \right)} \right)} \cos^{2}{\left(5 x \right)}}{\sin^{2}{\left(5 x \right)}} + \frac{8 \cos^{2}{\left(5 x \right)}}{\sin^{2}{\left(5 x \right)}}\right) \log{\left(\sin^{4}{\left(5 x \right)} \right)}$$

Simplify

The third derivative [src]

     /                                            2           2         2/   4     \         2         /   4     \\         
     |   2/   4     \         /   4     \   16*cos (5*x)   cos (5*x)*log \sin (5*x)/   12*cos (5*x)*log\sin (5*x)/|         
3000*|log \sin (5*x)/ - 12*log\sin (5*x)/ + ------------ + ------------------------- - ---------------------------|*cos(5*x)
     |                                          2                     2                            2              |         
     \                                       sin (5*x)             sin (5*x)                    sin (5*x)         /         
----------------------------------------------------------------------------------------------------------------------------
                                                          sin(5*x)

$$\frac{3000 \left(\log{\left(\sin^{4}{\left(5 x \right)} \right)}^{2} + \frac{\log{\left(\sin^{4}{\left(5 x \right)} \right)}^{2} \cos^{2}{\left(5 x \right)}}{\sin^{2}{\left(5 x \right)}} - 12 \log{\left(\sin^{4}{\left(5 x \right)} \right)} - \frac{12 \log{\left(\sin^{4}{\left(5 x \right)} \right)} \cos^{2}{\left(5 x \right)}}{\sin^{2}{\left(5 x \right)}} + \frac{16 \cos^{2}{\left(5 x \right)}}{\sin^{2}{\left(5 x \right)}}\right) \cos{\left(5 x \right)}}{\sin{\left(5 x \right)}}$$

Simplify

The graph

Other calculators

How to use it?

Identical expressions

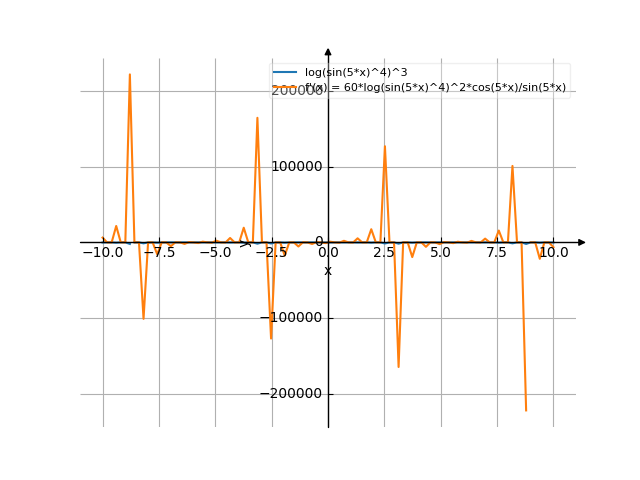
Derivative of ln(sin(5x)^4)^3

The graph:

Piecewise:

The solution