Derivative of 4-4sint
The solution
Detail solution
-
Differentiate term by term:
-
The derivative of the constant is zero.
-
The derivative of a constant times a function is the constant times the derivative of the function.
-
The derivative of sine is cosine:
So, the result is:
-
The result is:
-
The answer is:

 Derivative of -2x/(1+x^2)^2
Derivative of -2x/(1+x^2)^2
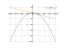 Derivative of y=√4-x^2
Derivative of y=√4-x^2
 Derivative of x^2/(x+2)
Derivative of x^2/(x+2)
 Derivative of (e^x+log(x))/(e^x-log(x))
Derivative of (e^x+log(x))/(e^x-log(x))