Derivative of (exp(2x)-1)/(exp(2x)+1)
The solution
2*x e - 1 -------- 2*x e + 1
(exp(2*x) - 1)/(exp(2*x) + 1)
-
Apply the quotient rule, which is:
and .
To find :
-
Differentiate term by term:
-
The derivative of the constant is zero.
-
Let .
-
The derivative of is itself.
-
-
Then, apply the chain rule. Multiply by :
-
The derivative of a constant times a function is the constant times the derivative of the function.
-
Apply the power rule: goes to
So, the result is:
-
The result of the chain rule is:
-
The result is:
-
To find :
-
Differentiate term by term:
-
The derivative of the constant is zero.
-
Let .
-
The derivative of is itself.
-
-
Then, apply the chain rule. Multiply by :
-
The derivative of a constant times a function is the constant times the derivative of the function.
-
Apply the power rule: goes to
So, the result is:
-
The result of the chain rule is:
-
The result is:
Now plug in to the quotient rule:
Now simplify:
The answer is:
2*x / 2*x \ 2*x
2*e 2*\e - 1/*e
-------- - -----------------
2*x 2
e + 1 / 2*x \
\e + 1/
/ / 2*x \ \
| | 2*e | / 2*x\|
| |1 - --------|*\-1 + e /|
| 2*x | 2*x| |
| 2*e \ 1 + e / | 2*x
4*|1 - -------- - --------------------------|*e
| 2*x 2*x |
\ 1 + e 1 + e /
--------------------------------------------------
2*x
1 + e
/ / 2*x 4*x \ \
| / 2*x\ | 6*e 6*e | / 2*x \ |
| \-1 + e /*|1 - -------- + -----------| | 2*e | 2*x|
| | 2*x 2| 3*|1 - --------|*e |
| 2*x | 1 + e / 2*x\ | | 2*x| |
| 3*e \ \1 + e / / \ 1 + e / | 2*x
8*|1 - -------- - ---------------------------------------- - ---------------------|*e
| 2*x 2*x 2*x |
\ 1 + e 1 + e 1 + e /
----------------------------------------------------------------------------------------
2*x
1 + e

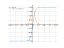 Derivative of tanh(x)
Derivative of tanh(x)
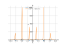 Derivative of tanx
Derivative of tanx
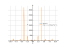 Derivative of tg2x
Derivative of tg2x
 Derivative of y=9
Derivative of y=9