Mister Exam

Other calculators

cos(arcsin(4x-8x^4))
The derivative of the function/ cos(arcsin(4x-8x^4))

Derivative of cos(arcsin(4x-8x^4))

Function f() - derivative -N order at the point
v

The graph:

from to

Piecewise:

The solution

You have entered [src] 
   /    /         4\\
cos\asin\4*x - 8*x //
cos⁡(asin⁡(−8x4+4x))\cos{\left(\operatorname{asin}{\left(- 8 x^{4} + 4 x \right)} \right)} 
d /   /    /         4\\\
--\cos\asin\4*x - 8*x ///
dx
ddxcos⁡(asin⁡(−8x4+4x))\frac{d}{d x} \cos{\left(\operatorname{asin}{\left(- 8 x^{4} + 4 x \right)} \right)}
Transform
The graph
02468-8-6-4-2-101020-10
Plot the graph f(x)
Plot the graph f'(x)
The first derivative [src] 
/        3\ /          4\
\4 - 32*x /*\-4*x + 8*x /
-------------------------
     ___________________ 
    /                 2  
   /      /         4\   
 \/   1 - \4*x - 8*x /
(−32x3+4)(8x4−4x)−(−8x4+4x)2+1\frac{\left(- 32 x^{3} + 4\right) \left(8 x^{4} - 4 x\right)}{\sqrt{- \left(- 8 x^{4} + 4 x\right)^{2} + 1}}
Simplify
The second derivative [src] 
    /                                                    2            2\
    |           2                           2 /        3\  /        3\ |
    |/        3\        3 /        3\   16*x *\-1 + 2*x / *\-1 + 8*x / |
-16*|\-1 + 8*x /  + 24*x *\-1 + 2*x / + -------------------------------|
    |                                                            2     |
    |                                                2 /       3\      |
    \                                        1 - 16*x *\1 - 2*x /      /
------------------------------------------------------------------------
                          _______________________                       
                         /                     2                        
                        /          2 /       3\                         
                      \/   1 - 16*x *\1 - 2*x /
−16⋅(16x2(2x3−1)2(8x3−1)2−16x2(−2x3+1)2+1+24x3⋅(2x3−1)+(8x3−1)2)−16x2(−2x3+1)2+1- \frac{16 \cdot \left(\frac{16 x^{2} \left(2 x^{3} - 1\right)^{2} \left(8 x^{3} - 1\right)^{2}}{- 16 x^{2} \left(- 2 x^{3} + 1\right)^{2} + 1} + 24 x^{3} \cdot \left(2 x^{3} - 1\right) + \left(8 x^{3} - 1\right)^{2}\right)}{\sqrt{- 16 x^{2} \left(- 2 x^{3} + 1\right)^{2} + 1}}
Simplify
The third derivative [src] 
       /                                                 3                                3            3                    2            \
       |                                      /        3\  /        3\       2 /        3\  /        3\        3 /        3\  /        3\|
       |    /        3\       /        3\   2*\-1 + 8*x / *\-1 + 2*x /   32*x *\-1 + 2*x / *\-1 + 8*x /    48*x *\-1 + 2*x / *\-1 + 8*x /|
-384*x*|2*x*\-1 + 2*x / + 3*x*\-1 + 8*x / + -------------------------- + ------------------------------- + ------------------------------|
       |                                                          2                                 2                              2     |
       |                                              2 /       3\           /                    2\                   2 /       3\      |
       |                                      1 - 16*x *\1 - 2*x /           |        2 /       3\ |           1 - 16*x *\1 - 2*x /      |
       \                                                                     \1 - 16*x *\1 - 2*x / /                                     /
------------------------------------------------------------------------------------------------------------------------------------------
                                                           _______________________                                                        
                                                          /                     2                                                         
                                                         /          2 /       3\                                                          
                                                       \/   1 - 16*x *\1 - 2*x /
−384x(32x2(2x3−1)3(8x3−1)3(−16x2(−2x3+1)2+1)2+48x3(2x3−1)2⋅(8x3−1)−16x2(−2x3+1)2+1+2⋅(2x3−1)(8x3−1)3−16x2(−2x3+1)2+1+2x(2x3−1)+3x(8x3−1))−16x2(−2x3+1)2+1- \frac{384 x \left(\frac{32 x^{2} \left(2 x^{3} - 1\right)^{3} \left(8 x^{3} - 1\right)^{3}}{\left(- 16 x^{2} \left(- 2 x^{3} + 1\right)^{2} + 1\right)^{2}} + \frac{48 x^{3} \left(2 x^{3} - 1\right)^{2} \cdot \left(8 x^{3} - 1\right)}{- 16 x^{2} \left(- 2 x^{3} + 1\right)^{2} + 1} + \frac{2 \cdot \left(2 x^{3} - 1\right) \left(8 x^{3} - 1\right)^{3}}{- 16 x^{2} \left(- 2 x^{3} + 1\right)^{2} + 1} + 2 x \left(2 x^{3} - 1\right) + 3 x \left(8 x^{3} - 1\right)\right)}{\sqrt{- 16 x^{2} \left(- 2 x^{3} + 1\right)^{2} + 1}}
Simplify
The graph
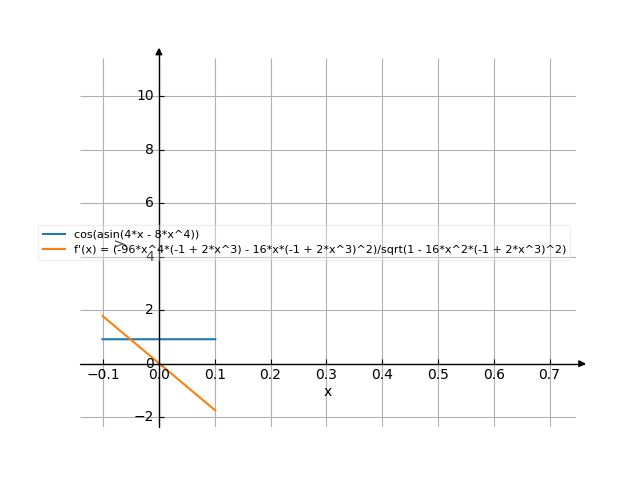
Derivative of cos(arcsin(4x-8x^4))
    © Mister Exam – Calculator