Mister Exam

Lang:

Other calculators

How to use it?
Derivative of:
Derivative of x^(4/5)
Derivative of 5*x^2-2/sqrt(x)+sin(pi/4)
Derivative of x^3-3*x
Derivative of x^3+2
Identical expressions
arctgx/sqrt(x)/(one +x^ two)
arctgx divide by square root of (x) divide by (1 plus x squared )
arctgx divide by square root of (x) divide by (one plus x to the power of two)
arctgx/√(x)/(1+x^2)
arctgx/sqrt(x)/(1+x2)
arctgx/sqrtx/1+x2
arctgx/sqrt(x)/(1+x²)
arctgx/sqrt(x)/(1+x to the power of 2)
arctgx/sqrtx/1+x^2
arctgx divide by sqrt(x) divide by (1+x^2)
Similar expressions
arctgx/sqrt(x)/(1-x^2)

The derivative of the function/ arctgx/sqrt(x)/(1+x^2)

Derivative of arctgx/sqrt(x)/(1+x^2)

The solution

You have entered [src]

   acot(x)    
--------------
  ___ /     2\
\/ x *\1 + x /

\frac{\operatorname{acot}{\left(x \right)}}{\sqrt{x} \left(x^{2} + 1\right)}

d /   acot(x)    \
--|--------------|
dx|  ___ /     2\|
  \\/ x *\1 + x //

\frac{d}{d x} \frac{\operatorname{acot}{\left(x \right)}}{\sqrt{x} \left(x^{2} + 1\right)}

Transform

The graph

Plot the graph f(x)

Plot the graph f'(x)

The first derivative [src]

         1              acot(x)         2*x*acot(x)  
- --------------- - --------------- - ---------------
                2      3/2 /     2\                 2
    ___ /     2\    2*x   *\1 + x /     ___ /     2\ 
  \/ x *\1 + x /                      \/ x *\1 + x /

- \frac{2 x \operatorname{acot}{\left(x \right)}}{\sqrt{x} \left(x^{2} + 1\right)^{2}} - \frac{1}{\sqrt{x} \left(x^{2} + 1\right)^{2}} - \frac{\operatorname{acot}{\left(x \right)}}{2 x^{\frac{3}{2}} \left(x^{2} + 1\right)}

Simplify

The second derivative [src]

                                                           /         2 \        
                                                           |      4*x  |        
                                                         2*|-1 + ------|*acot(x)
                     ___                                   |          2|        
      1          6*\/ x     3*acot(x)     2*acot(x)        \     1 + x /        
------------- + --------- + --------- + -------------- + -----------------------
 3/2 /     2\           2        5/2      ___ /     2\          ___ /     2\    
x   *\1 + x /   /     2\      4*x       \/ x *\1 + x /        \/ x *\1 + x /    
                \1 + x /                                                        
--------------------------------------------------------------------------------
                                          2                                     
                                     1 + x

\frac{\frac{2 \cdot \left(\frac{4 x^{2}}{x^{2} + 1} - 1\right) \operatorname{acot}{\left(x \right)}}{\sqrt{x} \left(x^{2} + 1\right)} + \frac{6 \sqrt{x}}{\left(x^{2} + 1\right)^{2}} + \frac{2 \operatorname{acot}{\left(x \right)}}{\sqrt{x} \left(x^{2} + 1\right)} + \frac{1}{x^{\frac{3}{2}} \left(x^{2} + 1\right)} + \frac{3 \operatorname{acot}{\left(x \right)}}{4 x^{\frac{5}{2}}}}{x^{2} + 1}

Simplify

The third derivative [src]

 /                                                               /         2 \                       /         2 \                    /         2 \        \ 
 |                                                               |      4*x  |                       |      4*x  |                ___ |      2*x  |        | 
 |                                                             8*|-1 + ------|                     3*|-1 + ------|*acot(x)   24*\/ x *|-1 + ------|*acot(x)| 
 |                       3/2                                     |          2|                       |          2|                    |          2|        | 
 |       9           12*x              9          15*acot(x)     \     1 + x /      9*acot(x)        \     1 + x /                    \     1 + x /        | 
-|--------------- + --------- + --------------- + ---------- + --------------- + --------------- + ----------------------- + ------------------------------| 
 |              2           3      5/2 /     2\        7/2                   2      3/2 /     2\         3/2 /     2\                          2           | 
 |  ___ /     2\    /     2\    4*x   *\1 + x /     8*x          ___ /     2\    2*x   *\1 + x /        x   *\1 + x /                  /     2\            | 
 \\/ x *\1 + x /    \1 + x /                                   \/ x *\1 + x /                                                          \1 + x /            / 
-------------------------------------------------------------------------------------------------------------------------------------------------------------
                                                                                 2                                                                           
                                                                            1 + x

- \frac{\frac{24 \sqrt{x} \left(\frac{2 x^{2}}{x^{2} + 1} - 1\right) \operatorname{acot}{\left(x \right)}}{\left(x^{2} + 1\right)^{2}} + \frac{12 x^{\frac{3}{2}}}{\left(x^{2} + 1\right)^{3}} + \frac{8 \cdot \left(\frac{4 x^{2}}{x^{2} + 1} - 1\right)}{\sqrt{x} \left(x^{2} + 1\right)^{2}} + \frac{3 \cdot \left(\frac{4 x^{2}}{x^{2} + 1} - 1\right) \operatorname{acot}{\left(x \right)}}{x^{\frac{3}{2}} \left(x^{2} + 1\right)} + \frac{9}{\sqrt{x} \left(x^{2} + 1\right)^{2}} + \frac{9 \operatorname{acot}{\left(x \right)}}{2 x^{\frac{3}{2}} \left(x^{2} + 1\right)} + \frac{9}{4 x^{\frac{5}{2}} \left(x^{2} + 1\right)} + \frac{15 \operatorname{acot}{\left(x \right)}}{8 x^{\frac{7}{2}}}}{x^{2} + 1}

Simplify

The graph

Other calculators

How to use it?

Identical expressions

Similar expressions

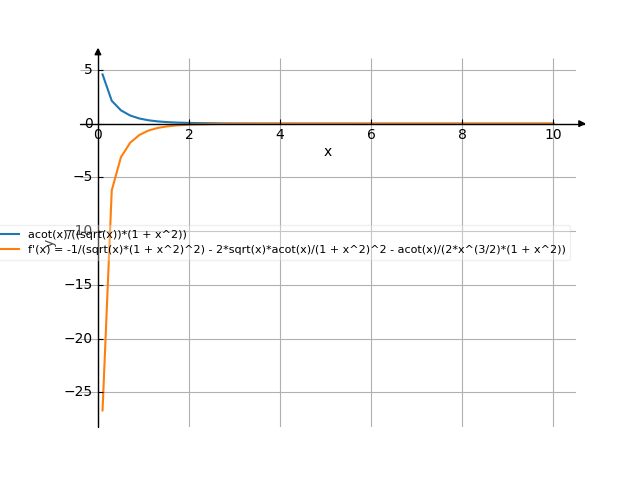
Derivative of arctgx/sqrt(x)/(1+x^2)

The graph:

Piecewise:

The solution