Mister Exam

Other calculators

arctg(x)^2+arctg^2x
The derivative of the function/ arctg(x)^2+arctg^2x

Derivative of arctg(x)^2+arctg^2x

Function f() - derivative -N order at the point
v

The graph:

from to

Piecewise:

The solution

You have entered [src] 
    2          2   
atan (x) + atan (x)
atan⁡2(x)+atan⁡2(x)\operatorname{atan}^{2}{\left(x \right)} + \operatorname{atan}^{2}{\left(x \right)} 
d /    2          2   \
--\atan (x) + atan (x)/
dx
ddx(atan⁡2(x)+atan⁡2(x))\frac{d}{d x} \left(\operatorname{atan}^{2}{\left(x \right)} + \operatorname{atan}^{2}{\left(x \right)}\right)
Transform
The graph
02468-8-6-4-2-10105-5
Plot the graph f(x)
Plot the graph f'(x)
The first derivative [src] 
4*atan(x)
---------
       2 
  1 + x
4atan⁡(x)x2+1\frac{4 \operatorname{atan}{\left(x \right)}}{x^{2} + 1}
Simplify
The second derivative [src] 
4*(1 - 2*x*atan(x))
-------------------
             2     
     /     2\      
     \1 + x /
4(−2xatan⁡(x)+1)(x2+1)2\frac{4 \left(- 2 x \operatorname{atan}{\left(x \right)} + 1\right)}{\left(x^{2} + 1\right)^{2}}
Simplify
The third derivative [src] 
  /                       2        \
  |            3*x     4*x *atan(x)|
8*|-atan(x) - ------ + ------------|
  |                2           2   |
  \           1 + x       1 + x    /
------------------------------------
                     2              
             /     2\               
             \1 + x /
8⋅(4x2atan⁡(x)x2+1−atan⁡(x)−3xx2+1)(x2+1)2\frac{8 \cdot \left(\frac{4 x^{2} \operatorname{atan}{\left(x \right)}}{x^{2} + 1} - \operatorname{atan}{\left(x \right)} - \frac{3 x}{x^{2} + 1}\right)}{\left(x^{2} + 1\right)^{2}}
Simplify
The graph
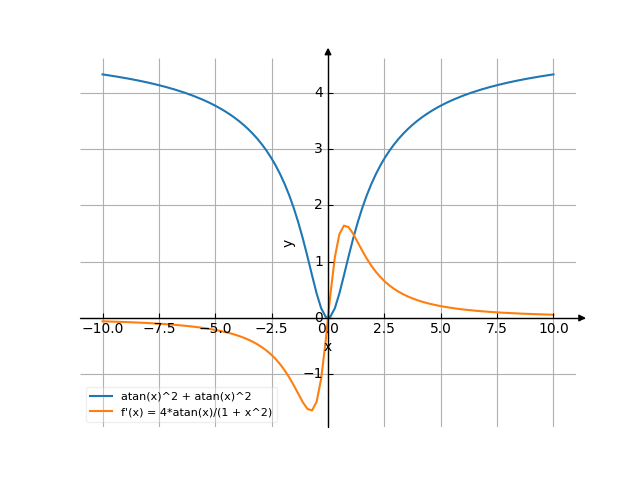
Derivative of arctg(x)^2+arctg^2x
    © Mister Exam – Calculator