Mister Exam

Other calculators

arcctg(((x-3))/((x^2)+4))
The derivative of the function/ arcctg(((x-3))/((x^2)+4))

Derivative of arcctg(((x-3))/((x^2)+4))

Function f() - derivative -N order at the point
v

The graph:

from to

Piecewise:

The solution

You have entered [src] 
    /x - 3 \
acot|------|
    | 2    |
    \x  + 4/
acot⁡(x−3x2+4)\operatorname{acot}{\left(\frac{x - 3}{x^{2} + 4} \right)} 
d /    /x - 3 \\
--|acot|------||
dx|    | 2    ||
  \    \x  + 4//
ddxacot⁡(x−3x2+4)\frac{d}{d x} \operatorname{acot}{\left(\frac{x - 3}{x^{2} + 4} \right)}
Transform
The graph
02468-8-6-4-2-10105-5
Plot the graph f(x)
Plot the graph f'(x)
The first derivative [src] 
 /  1      2*x*(x - 3)\ 
-|------ - -----------| 
 | 2                2 | 
 |x  + 4    / 2    \  | 
 \          \x  + 4/  / 
------------------------
                 2      
          (x - 3)       
     1 + ---------      
                 2      
         / 2    \       
         \x  + 4/
−−2x(x−3)(x2+4)2+1x2+4(x−3)2(x2+4)2+1- \frac{- \frac{2 x \left(x - 3\right)}{\left(x^{2} + 4\right)^{2}} + \frac{1}{x^{2} + 4}}{\frac{\left(x - 3\right)^{2}}{\left(x^{2} + 4\right)^{2}} + 1}
Simplify
The second derivative [src] 
  /                                              2         \
  |                           /     2*x*(-3 + x)\          |
  |                           |-1 + ------------| *(-3 + x)|
  |              2            |             2   |          |
  |           4*x *(-3 + x)   \        4 + x    /          |
2*|-3 + 3*x - ------------- + -----------------------------|
  |                    2         /            2\           |
  |               4 + x          |    (-3 + x) | /     2\  |
  |                              |1 + ---------|*\4 + x /  |
  |                              |            2|           |
  |                              |    /     2\ |           |
  \                              \    \4 + x / /           /
------------------------------------------------------------
                 /            2\         2                  
                 |    (-3 + x) | /     2\                   
                 |1 + ---------|*\4 + x /                   
                 |            2|                            
                 |    /     2\ |                            
                 \    \4 + x / /
2(−4x2(x−3)x2+4+3x+(x−3)(2x(x−3)x2+4−1)2(x2+4)((x−3)2(x2+4)2+1)−3)(x2+4)2((x−3)2(x2+4)2+1)\frac{2 \left(- \frac{4 x^{2} \left(x - 3\right)}{x^{2} + 4} + 3 x + \frac{\left(x - 3\right) \left(\frac{2 x \left(x - 3\right)}{x^{2} + 4} - 1\right)^{2}}{\left(x^{2} + 4\right) \left(\frac{\left(x - 3\right)^{2}}{\left(x^{2} + 4\right)^{2}} + 1\right)} - 3\right)}{\left(x^{2} + 4\right)^{2} \left(\frac{\left(x - 3\right)^{2}}{\left(x^{2} + 4\right)^{2}} + 1\right)}
Simplify
The third derivative [src] 
  /                                                                  /              2                      2         2\                                                                                               \
  |                                              /     2*x*(-3 + x)\ |    2*(-3 + x)    8*x*(-3 + x)   12*x *(-3 + x) |                        3                                            /              2         \|
  |                                              |-1 + ------------|*|1 - ----------- - ------------ + ---------------|     /     2*x*(-3 + x)\          2     /     2*x*(-3 + x)\          |           4*x *(-3 + x)||
  |                                              |             2   | |            2             2                 2   |   4*|-1 + ------------| *(-3 + x)    4*|-1 + ------------|*(-3 + x)*|-3 + 3*x - -------------||
  |        2                        3            \        4 + x    / |       4 + x         4 + x          /     2\    |     |             2   |                |             2   |          |                    2   ||
  |    12*x     12*x*(-3 + x)   24*x *(-3 + x)                       \                                    \4 + x /    /     \        4 + x    /                \        4 + x    /          \               4 + x    /|
2*|3 - ------ - ------------- + -------------- - ---------------------------------------------------------------------- + -------------------------------- + ---------------------------------------------------------|
  |         2            2                2                             /            2\                                                     2                                /            2\         2                |
  |    4 + x        4 + x         /     2\                              |    (-3 + x) | /     2\                             /            2\          3                      |    (-3 + x) | /     2\                 |
  |                               \4 + x /                              |1 + ---------|*\4 + x /                             |    (-3 + x) |  /     2\                       |1 + ---------|*\4 + x /                 |
  |                                                                     |            2|                                      |1 + ---------| *\4 + x /                       |            2|                          |
  |                                                                     |    /     2\ |                                      |            2|                                 |    /     2\ |                          |
  |                                                                     \    \4 + x / /                                      |    /     2\ |                                 \    \4 + x / /                          |
  \                                                                                                                          \    \4 + x / /                                                                          /
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
                                                                                               /            2\         2                                                                                               
                                                                                               |    (-3 + x) | /     2\                                                                                                
                                                                                               |1 + ---------|*\4 + x /                                                                                                
                                                                                               |            2|                                                                                                         
                                                                                               |    /     2\ |                                                                                                         
                                                                                               \    \4 + x / /
2⋅(24x3(x−3)(x2+4)2−12x2x2+4−12x(x−3)x2+4+4(x−3)2(2x(x−3)x2+4−1)3(x2+4)3((x−3)2(x2+4)2+1)2+4(x−3)(2x(x−3)x2+4−1)(−4x2(x−3)x2+4+3x−3)(x2+4)2((x−3)2(x2+4)2+1)+3−(2x(x−3)x2+4−1)(12x2(x−3)2(x2+4)2−8x(x−3)x2+4−2(x−3)2x2+4+1)(x2+4)((x−3)2(x2+4)2+1))(x2+4)2((x−3)2(x2+4)2+1)\frac{2 \cdot \left(\frac{24 x^{3} \left(x - 3\right)}{\left(x^{2} + 4\right)^{2}} - \frac{12 x^{2}}{x^{2} + 4} - \frac{12 x \left(x - 3\right)}{x^{2} + 4} + \frac{4 \left(x - 3\right)^{2} \left(\frac{2 x \left(x - 3\right)}{x^{2} + 4} - 1\right)^{3}}{\left(x^{2} + 4\right)^{3} \left(\frac{\left(x - 3\right)^{2}}{\left(x^{2} + 4\right)^{2}} + 1\right)^{2}} + \frac{4 \left(x - 3\right) \left(\frac{2 x \left(x - 3\right)}{x^{2} + 4} - 1\right) \left(- \frac{4 x^{2} \left(x - 3\right)}{x^{2} + 4} + 3 x - 3\right)}{\left(x^{2} + 4\right)^{2} \left(\frac{\left(x - 3\right)^{2}}{\left(x^{2} + 4\right)^{2}} + 1\right)} + 3 - \frac{\left(\frac{2 x \left(x - 3\right)}{x^{2} + 4} - 1\right) \left(\frac{12 x^{2} \left(x - 3\right)^{2}}{\left(x^{2} + 4\right)^{2}} - \frac{8 x \left(x - 3\right)}{x^{2} + 4} - \frac{2 \left(x - 3\right)^{2}}{x^{2} + 4} + 1\right)}{\left(x^{2} + 4\right) \left(\frac{\left(x - 3\right)^{2}}{\left(x^{2} + 4\right)^{2}} + 1\right)}\right)}{\left(x^{2} + 4\right)^{2} \left(\frac{\left(x - 3\right)^{2}}{\left(x^{2} + 4\right)^{2}} + 1\right)}
Simplify
The graph
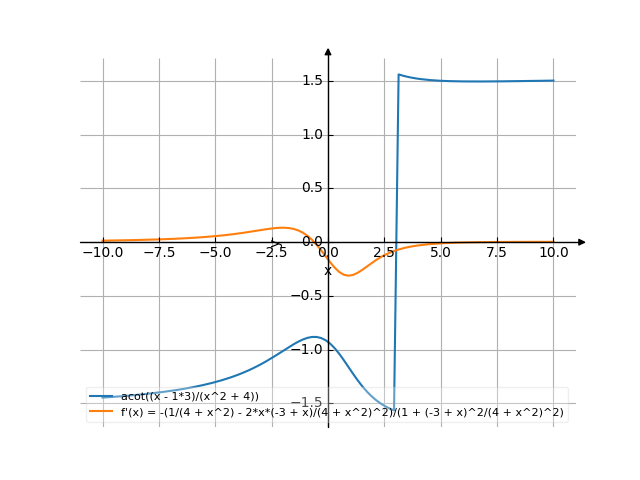
Derivative of arcctg(((x-3))/((x^2)+4))
    © Mister Exam – Calculator