Mister Exam

Other calculators

arcsin(x/(sqrt(1-x^2)))

  • How to use it?

  • Derivative of:
  • Derivative of 8/x Derivative of 8/x
  • Derivative of x^2-2 Derivative of x^2-2
  • Derivative of tg6x Derivative of tg6x
  • Derivative of 4/x^6 Derivative of 4/x^6

  • Identical expressions

  • arcsin(x/(sqrt(one -x^ two)))
  • arc sinus of (x divide by ( square root of (1 minus x squared )))
  • arc sinus of (x divide by ( square root of (one minus x to the power of two)))
  • arcsin(x/(√(1-x^2)))
  • arcsin(x/(sqrt(1-x2)))
  • arcsinx/sqrt1-x2
  • arcsin(x/(sqrt(1-x²)))
  • arcsin(x/(sqrt(1-x to the power of 2)))
  • arcsinx/sqrt1-x^2
  • arcsin(x divide by (sqrt(1-x^2)))

  • Similar expressions

  • arcsin(x/(sqrt(1+x^2)))
The derivative of the function/ arcsin(x/(sqrt(1-x^2)))

Derivative of arcsin(x/(sqrt(1-x^2)))

Function f() - derivative -N order at the point
v

The graph:

from to

Piecewise:

The solution

You have entered [src] 
    /     x     \
asin|-----------|
    |   ________|
    |  /      2 |
    \\/  1 - x  /
asin⁡(x−x2+1)\operatorname{asin}{\left(\frac{x}{\sqrt{- x^{2} + 1}} \right)} 
d /    /     x     \\
--|asin|-----------||
dx|    |   ________||
  |    |  /      2 ||
  \    \\/  1 - x  //
ddxasin⁡(x−x2+1)\frac{d}{d x} \operatorname{asin}{\left(\frac{x}{\sqrt{- x^{2} + 1}} \right)}
Transform
The graph
02468-8-6-4-2-1010400-200
Plot the graph f(x)
Plot the graph f'(x)
The first derivative [src] 
                    2    
     1             x     
----------- + -----------
   ________           3/2
  /      2    /     2\   
\/  1 - x     \1 - x /   
-------------------------
          ____________   
         /        2      
        /        x       
       /   1 - ------    
      /             2    
    \/         1 - x
x2(−x2+1)32+1−x2+1−x2−x2+1+1\frac{\frac{x^{2}}{\left(- x^{2} + 1\right)^{\frac{3}{2}}} + \frac{1}{\sqrt{- x^{2} + 1}}}{\sqrt{- \frac{x^{2}}{- x^{2} + 1} + 1}}
Simplify
The second derivative [src] 
  /                                 /       2  \ /         2  \\
  |                                 |      x   | |        x   ||
  |                                 |1 + ------|*|-1 + -------||
  |                           2     |         2| |           2||
  |     1        2         3*x      \    1 - x / \     -1 + x /|
x*|- ------- + ------ + --------- + ---------------------------|
  |        2        2           2      /       2  \            |
  |  -1 + x    1 - x    /     2\       |      x   | /      2\  |
  |                     \1 - x /       |1 - ------|*\-1 + x /  |
  |                                    |         2|            |
  \                                    \    1 - x /            /
----------------------------------------------------------------
                                   ____________                 
                    ________      /        2                    
                   /      2      /        x                     
                 \/  1 - x  *   /   1 - ------                  
                               /             2                  
                             \/         1 - x
x(3x2(−x2+1)2+(x2−x2+1+1)(x2x2−1−1)(x2−1)(−x2−x2+1+1)−1x2−1+2−x2+1)−x2+1−x2−x2+1+1\frac{x \left(\frac{3 x^{2}}{\left(- x^{2} + 1\right)^{2}} + \frac{\left(\frac{x^{2}}{- x^{2} + 1} + 1\right) \left(\frac{x^{2}}{x^{2} - 1} - 1\right)}{\left(x^{2} - 1\right) \left(- \frac{x^{2}}{- x^{2} + 1} + 1\right)} - \frac{1}{x^{2} - 1} + \frac{2}{- x^{2} + 1}\right)}{\sqrt{- x^{2} + 1} \sqrt{- \frac{x^{2}}{- x^{2} + 1} + 1}}
Simplify
The third derivative [src] 
  /          4         2 \   /       2  \ /         2          4   \        /         2  \ /                           2  \                      2             
  |       5*x       6*x  |   |      x   | |      5*x        4*x    |      2 |        x   | |     1        2         3*x   |        /         2  \  /       2  \
3*|1 + --------- + ------|   |1 + ------|*|1 - ------- + ----------|   2*x *|-1 + -------|*|- ------- + ------ + ---------|      2 |        x   |  |      x   |
  |            2        2|   |         2| |          2            2|        |           2| |        2        2           2|   3*x *|-1 + -------| *|1 + ------|
  |    /     2\    1 - x |   \    1 - x / |    -1 + x    /      2\ |        \     -1 + x / |  -1 + x    1 - x    /     2\ |        |           2|  |         2|
  \    \1 - x /          /                \              \-1 + x / /                       \                     \1 - x / /        \     -1 + x /  \    1 - x /
-------------------------- - --------------------------------------- + ---------------------------------------------------- + ---------------------------------
               2                      /       2  \                                    /       2  \                                             2               
          1 - x                       |      x   | /      2\                          |      x   | /      2\                       /       2  \           2    
                                      |1 - ------|*\-1 + x /                          |1 - ------|*\-1 + x /                       |      x   |  /      2\     
                                      |         2|                                    |         2|                                 |1 - ------| *\-1 + x /     
                                      \    1 - x /                                    \    1 - x /                                 |         2|                
                                                                                                                                   \    1 - x /                
---------------------------------------------------------------------------------------------------------------------------------------------------------------
                                                                                   ____________                                                                
                                                                    ________      /        2                                                                   
                                                                   /      2      /        x                                                                    
                                                                 \/  1 - x  *   /   1 - ------                                                                 
                                                                               /             2                                                                 
                                                                             \/         1 - x
2x2(x2x2−1−1)(3x2(−x2+1)2−1x2−1+2−x2+1)(x2−1)(−x2−x2+1+1)+3x2(x2−x2+1+1)(x2x2−1−1)2(x2−1)2(−x2−x2+1+1)2−(x2−x2+1+1)(4x4(x2−1)2−5x2x2−1+1)(x2−1)(−x2−x2+1+1)+3⋅(5x4(−x2+1)2+6x2−x2+1+1)−x2+1−x2+1−x2−x2+1+1\frac{\frac{2 x^{2} \left(\frac{x^{2}}{x^{2} - 1} - 1\right) \left(\frac{3 x^{2}}{\left(- x^{2} + 1\right)^{2}} - \frac{1}{x^{2} - 1} + \frac{2}{- x^{2} + 1}\right)}{\left(x^{2} - 1\right) \left(- \frac{x^{2}}{- x^{2} + 1} + 1\right)} + \frac{3 x^{2} \left(\frac{x^{2}}{- x^{2} + 1} + 1\right) \left(\frac{x^{2}}{x^{2} - 1} - 1\right)^{2}}{\left(x^{2} - 1\right)^{2} \left(- \frac{x^{2}}{- x^{2} + 1} + 1\right)^{2}} - \frac{\left(\frac{x^{2}}{- x^{2} + 1} + 1\right) \left(\frac{4 x^{4}}{\left(x^{2} - 1\right)^{2}} - \frac{5 x^{2}}{x^{2} - 1} + 1\right)}{\left(x^{2} - 1\right) \left(- \frac{x^{2}}{- x^{2} + 1} + 1\right)} + \frac{3 \cdot \left(\frac{5 x^{4}}{\left(- x^{2} + 1\right)^{2}} + \frac{6 x^{2}}{- x^{2} + 1} + 1\right)}{- x^{2} + 1}}{\sqrt{- x^{2} + 1} \sqrt{- \frac{x^{2}}{- x^{2} + 1} + 1}}
Simplify
The graph
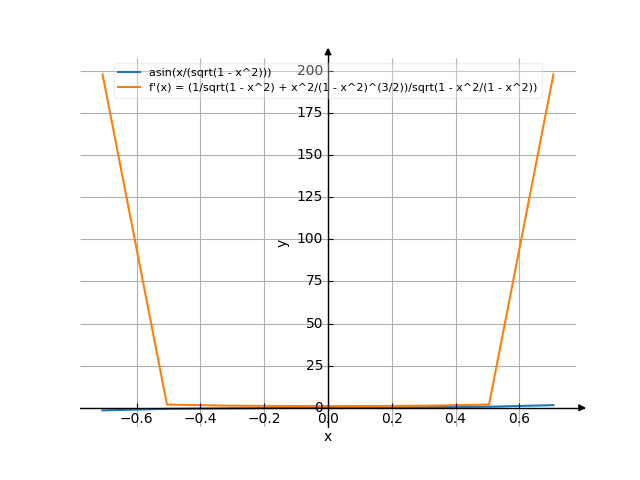
Derivative of arcsin(x/(sqrt(1-x^2)))
    © Mister Exam – Calculator