Mister Exam

Other calculators

arcsin^2(sqrt(x))
The derivative of the function/ arcsin^2(sqrt(x))

Derivative of arcsin^2(sqrt(x))

Function f() - derivative -N order at the point
v

The graph:

from to

Piecewise:

The solution

You have entered [src] 
    2/  ___\
asin \\/ x /
asin⁡2(x)\operatorname{asin}^{2}{\left(\sqrt{x} \right)} 
d /    2/  ___\\
--\asin \\/ x //
dx
ddxasin⁡2(x)\frac{d}{d x} \operatorname{asin}^{2}{\left(\sqrt{x} \right)}
Transform
The graph
02468-8-6-4-2-1010-1010
Plot the graph f(x)
Plot the graph f'(x)
The first derivative [src] 
      /  ___\  
  asin\\/ x /  
---------------
  ___   _______
\/ x *\/ 1 - x
asin⁡(x)x−x+1\frac{\operatorname{asin}{\left(\sqrt{x} \right)}}{\sqrt{x} \sqrt{- x + 1}}
Simplify
The second derivative [src] 
                     /  ___\           /  ___\  
      1          asin\\/ x /       asin\\/ x /  
- ---------- + ---------------- - --------------
  x*(-1 + x)     ___        3/2    3/2   _______
               \/ x *(1 - x)      x   *\/ 1 - x 
------------------------------------------------
                       2
−1x(x−1)+asin⁡(x)x(−x+1)32−asin⁡(x)x32−x+12\frac{- \frac{1}{x \left(x - 1\right)} + \frac{\operatorname{asin}{\left(\sqrt{x} \right)}}{\sqrt{x} \left(- x + 1\right)^{\frac{3}{2}}} - \frac{\operatorname{asin}{\left(\sqrt{x} \right)}}{x^{\frac{3}{2}} \sqrt{- x + 1}}}{2}
Simplify
The third derivative [src] 
                                   /  ___\          /  ___\           /  ___\  
     3             3         2*asin\\/ x /    3*asin\\/ x /     3*asin\\/ x /  
----------- + ----------- - --------------- + -------------- + ----------------
          2    2             3/2        3/2    5/2   _______     ___        5/2
x*(-1 + x)    x *(-1 + x)   x   *(1 - x)      x   *\/ 1 - x    \/ x *(1 - x)   
-------------------------------------------------------------------------------
                                       4
3x(x−1)2+3x2(x−1)+3asin⁡(x)x(−x+1)52−2asin⁡(x)x32(−x+1)32+3asin⁡(x)x52−x+14\frac{\frac{3}{x \left(x - 1\right)^{2}} + \frac{3}{x^{2} \left(x - 1\right)} + \frac{3 \operatorname{asin}{\left(\sqrt{x} \right)}}{\sqrt{x} \left(- x + 1\right)^{\frac{5}{2}}} - \frac{2 \operatorname{asin}{\left(\sqrt{x} \right)}}{x^{\frac{3}{2}} \left(- x + 1\right)^{\frac{3}{2}}} + \frac{3 \operatorname{asin}{\left(\sqrt{x} \right)}}{x^{\frac{5}{2}} \sqrt{- x + 1}}}{4}
Simplify
The graph
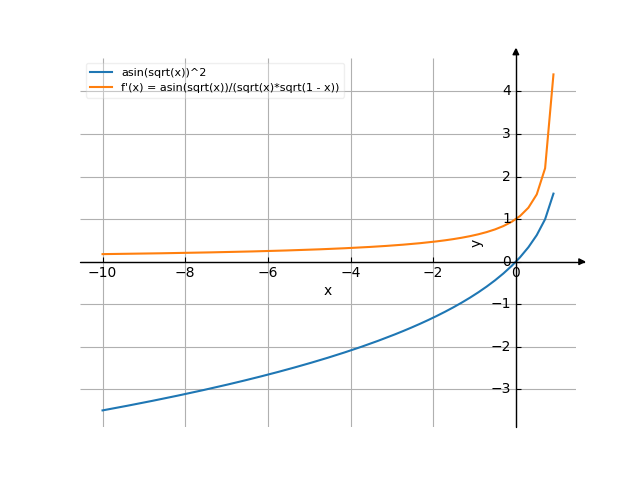
Derivative of arcsin^2(sqrt(x))
    © Mister Exam – Calculator