Mister Exam

Other calculators

arccos8x^3
The derivative of the function/ arccos8x^3

Derivative of arccos8x^3

Function f() - derivative -N order at the point
v

The graph:

from to

Piecewise:

The solution

You have entered [src] 
    3     
acos (8*x)
acos⁡3(8x)\operatorname{acos}^{3}{\left(8 x \right)} 
d /    3     \
--\acos (8*x)/
dx
ddxacos⁡3(8x)\frac{d}{d x} \operatorname{acos}^{3}{\left(8 x \right)}
Transform
The graph
02468-8-6-4-2-1010-500250
Plot the graph f(x)
Plot the graph f'(x)
The first derivative [src] 
        2     
-24*acos (8*x)
--------------
   ___________
  /         2 
\/  1 - 64*x
−24acos⁡2(8x)1−64x2- \frac{24 \operatorname{acos}^{2}{\left(8 x \right)}}{\sqrt{1 - 64 x^{2}}}
Simplify
The second derivative [src] 
     /    1        4*x*acos(8*x) \          
-384*|---------- + --------------|*acos(8*x)
     |         2              3/2|          
     |-1 + 64*x    /        2\   |          
     \             \1 - 64*x /   /
−384⋅(4xacos⁡(8x)(1−64x2)32+164x2−1)acos⁡(8x)- 384 \cdot \left(\frac{4 x \operatorname{acos}{\left(8 x \right)}}{\left(1 - 64 x^{2}\right)^{\frac{3}{2}}} + \frac{1}{64 x^{2} - 1}\right) \operatorname{acos}{\left(8 x \right)}
Simplify
The third derivative [src] 
     /                         2               2     2                      \
     |        2            acos (8*x)     192*x *acos (8*x)   48*x*acos(8*x)|
1536*|- -------------- - -------------- - ----------------- + --------------|
     |             3/2              3/2                5/2                2 |
     |  /        2\      /        2\        /        2\       /         2\  |
     \  \1 - 64*x /      \1 - 64*x /        \1 - 64*x /       \-1 + 64*x /  /
1536(−192x2acos⁡2(8x)(1−64x2)52+48xacos⁡(8x)(64x2−1)2−acos⁡2(8x)(1−64x2)32−2(1−64x2)32)1536 \left(- \frac{192 x^{2} \operatorname{acos}^{2}{\left(8 x \right)}}{\left(1 - 64 x^{2}\right)^{\frac{5}{2}}} + \frac{48 x \operatorname{acos}{\left(8 x \right)}}{\left(64 x^{2} - 1\right)^{2}} - \frac{\operatorname{acos}^{2}{\left(8 x \right)}}{\left(1 - 64 x^{2}\right)^{\frac{3}{2}}} - \frac{2}{\left(1 - 64 x^{2}\right)^{\frac{3}{2}}}\right)
Simplify
The graph
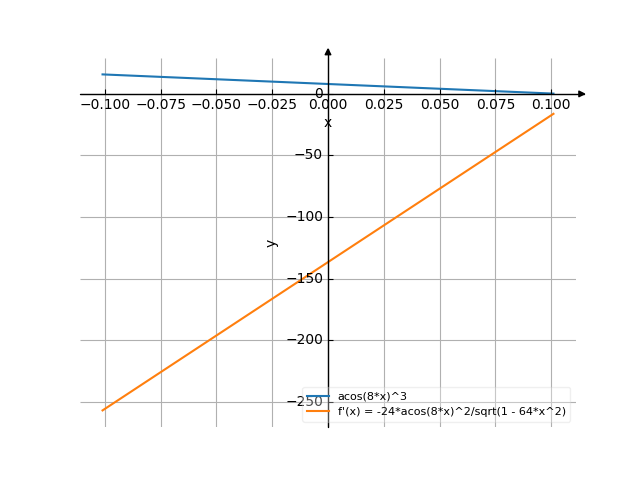
Derivative of arccos8x^3
    © Mister Exam – Calculator