Derivative of 3x^2*arcsin(2x-1)
The solution
You have entered
[src]
2 3*x *asin(2*x - 1)
$$3 x^{2} \operatorname{asin}{\left(2 x - 1 \right)}$$
d / 2 \ --\3*x *asin(2*x - 1)/ dx
$$\frac{d}{d x} 3 x^{2} \operatorname{asin}{\left(2 x - 1 \right)}$$
The first derivative
[src]
2
6*x
6*x*asin(2*x - 1) + -------------------
________________
/ 2
\/ 1 - (2*x - 1)
$$\frac{6 x^{2}}{\sqrt{1 - \left(2 x - 1\right)^{2}}} + 6 x \operatorname{asin}{\left(2 x - 1 \right)}$$
The second derivative
[src]
/ 2 \ | 4*x 2*x *(-1 + 2*x) | 6*|-------------------- + -------------------- + asin(-1 + 2*x)| | _________________ 3/2 | | / 2 / 2\ | \\/ 1 - (-1 + 2*x) \1 - (-1 + 2*x) / /
$$6 \cdot \left(\frac{2 x^{2} \cdot \left(2 x - 1\right)}{\left(1 - \left(2 x - 1\right)^{2}\right)^{\frac{3}{2}}} + \frac{4 x}{\sqrt{1 - \left(2 x - 1\right)^{2}}} + \operatorname{asin}{\left(2 x - 1 \right)}\right)$$
The third derivative
[src]
/ / 2 \ \
| 2 | 3*(-1 + 2*x) | |
| 2*x *|-1 + ----------------| |
| | 2| |
| \ -1 + (-1 + 2*x) / 6*x*(-1 + 2*x)|
12*|3 - ---------------------------- + ---------------|
| 2 2|
\ 1 - (-1 + 2*x) 1 - (-1 + 2*x) /
-------------------------------------------------------
_________________
/ 2
\/ 1 - (-1 + 2*x)
$$\frac{12 \left(- \frac{2 x^{2} \cdot \left(\frac{3 \left(2 x - 1\right)^{2}}{\left(2 x - 1\right)^{2} - 1} - 1\right)}{1 - \left(2 x - 1\right)^{2}} + \frac{6 x \left(2 x - 1\right)}{1 - \left(2 x - 1\right)^{2}} + 3\right)}{\sqrt{1 - \left(2 x - 1\right)^{2}}}$$
The graph
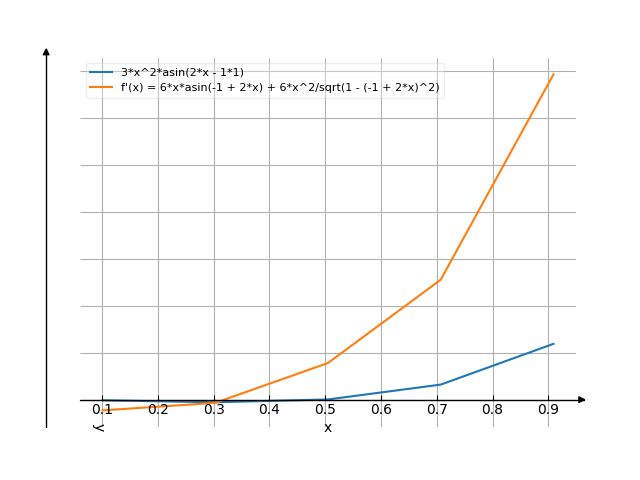

![Find the derivative of y' = f'(x) = 3x²*arcsin(2x-1) (3x squared multiply by arc sinus of (2x minus 1)) - functions. Find the derivative of the function at the point. [THERE'S THE ANSWER!] 3x^2*arcsin(2x-1)](/media/krcore-image-pods/176/hash/derivative/2/4b/bc691d30fa5b7c7454c86e29a3490.png)
 Derivative of 13*x-13*tan(x)-18
Derivative of 13*x-13*tan(x)-18
 Derivative of (0,5-x)cosx+sinx
Derivative of (0,5-x)cosx+sinx
 Derivative of x+9
Derivative of x+9
 Derivative of x/6
Derivative of x/6