按步骤的级数求和

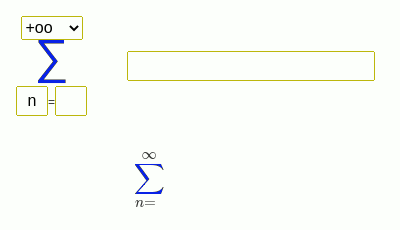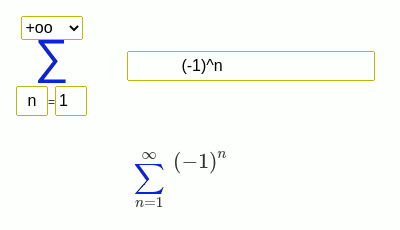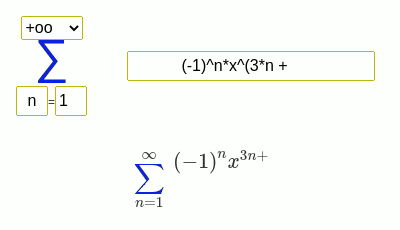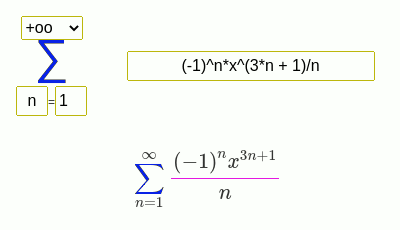
级数求和示例

级数求和计算器能做什么？

输入求和式、首项与末项；若求无穷和则设为无穷.

• 计算部分和
• 级数和的极限
• 判定收敛性:
  • 发散
  • 绝对收敛. 收敛级数
  • 条件收敛
  • 一致收敛
  • 收敛的必要条件
  • 莱布尼茨判别法
  • 魏尔斯特拉斯判别法
  • 阿贝尔判别法
  • 狄利克雷判别法
  • 极限比较判别法
  • 极限比较判别法
  • 望远镜法（柯西凝聚判别）
  • 柯西—麦克劳林积分判别
  • 比较判别法
  • 拉贝—迪亚梅尔判别法
• 支持:
  • 函数项级数:

    含变量 x 或 z

    • 幂级数
    • 泰勒级数
    • 麦克劳林级数
    • 傅里叶级数
    • 三角级数
    • 洛朗级数
  • 交错级数 / 变号级数
  • 倒数平方级数
  • 调和级数
  • 格兰迪级数
  • 弗林特希尔斯级数
  • 肯普纳级数
  • 收敛级数
  • 发散级数
  • 正项级数
  • 部分级数
  • 其他
• 计算:
  • 级数之和
  • 级数的数值和
  • 级数的收敛速度
  • 幂级数的收敛半径
• 绘制图像:
  • 部分和
  • 级数的极限

详细了解 级数和.

上述示例还包含:

• 绝对值 或 绝对值: absolute(x) 或 |x|
• 平方根 sqrt(x),
  立方根 cbrt(x)
• 三角函数:
  正弦 sin(x), 余弦 cos(x), 正切 tan(x), 余切 ctan(x)
• 指数函数与指数 exp(x)
• 反三角函数:
  反正弦 asin(x), 反余弦 acos(x), 反正切 atan(x), 反余切 acot(x)
• 自然对数 ln(x),
  常用对数 log(x)
• 双曲函数:
  双曲正弦 sh(x), 双曲余弦 ch(x), 双曲正切与双曲余切 tanh(x), ctanh(x)
• 反双曲函数:
  反双曲正弦 asinh(x), 反双曲余弦 acosh(x), 反双曲正切 atanh(x), 反双曲余切 acoth(x)
• 其他三角与双曲函数:
  正割 sec(x), 余割 csc(x), 反正割 asec(x), 反余割 acsc(x), 双曲正割 sech(x), 双曲余割 csch(x), 反双曲正割 asech(x), 反双曲余割 acsch(x)
• 取整函数:
  向下取整 floor(x), 向上取整 ceiling(x)
• 数的符号:
  sign(x)
• 概率论相关:
  误差函数 erf(x) (概率积分), 拉普拉斯函数 laplace(x)
• 阶乘 x:
  x! 或 factorial(x)
• 伽马函数 gamma(x)
• 朗伯特 W 函数 LambertW(x)
• 三角积分: Si(x), Ci(x), Shi(x), Chi(x)

输入规则

可进行以下运算

2*x

- 乘法

3/x

- 除法

x^2

- 平方

x^3

- 立方

x^5

- 幂运算

x + 7

- 加法

x - 6

- 减法

实数

以如下形式输入 7.5, 不 7,5

常数

pi

- 圆周率

e

- 自然对数的底

i

- 虚数单位

oo

- 无穷符号