Mister Exam
Other calculators
- Canonical form of a elliptical paraboloid
- Canonical form of a double hyperboloid
- Canonical form of a imaginary ellipsoid
- Canonical form of a degenerate ellipse
- Canonical form of a parabola
-
How to use it?
- Plot:
- tan(x^2+y^2)=1
- x^2+4*y^2=16
- z=x^2-2*y^2+4*x*y-6*x+5
- (x^2+y^2-1)-x^2*y^3=0
- Canonical form:
- x1x2+x2x3+x1x3
- x1x2+x1x3=0
- 3x^2+2y^2-4z^2=0
- 8x^2+7y^2+3z^2+12xy+4xz-8yz
Bring to Canonical Form
What can a canonical calculator do?
- For a given equation it finds:
- Canonical form of the equation (for lines and surfaces of second order)
- Basis-vector of canonical coordinate system (for 2nd order lines)
- Center of canonical coordinate system (for 2nd order lines)
- Detailed Solution in Two Ways:
- Direct method with transition to a new center of coordinates and rotation around a new center of coordinates (for lines)
- Method of invariants with calculation of a set of determinants (for lines and surfaces)
- Plot a graph of the second order line, plot the center of the canonical system and the basis vectors of the canonical system
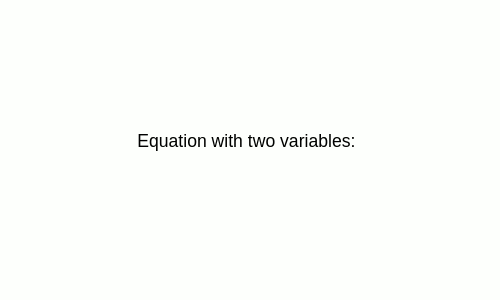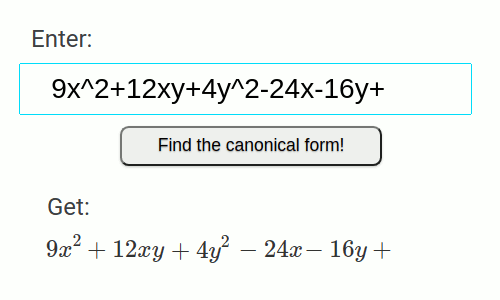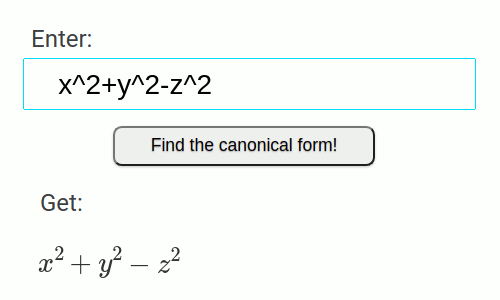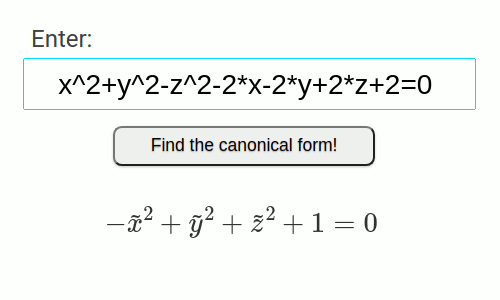
Examples
- Two parallel straight lines
9x^2+12xy+4y^2-24x-16y+3=0
- Parabola
x^2-2xy+y^2-10x-6y+25=0
- Degenerate Ellipse
5x^2+4xy+y^2-6x-2y+2=0
- Ellipse
5*x^2+4*x*y+8*y^2+8*x+14*y+5=0
- Imaginary Ellipse
8063 - 250*y - 10*x + 50*x^2 + 50*y^2
- Ellipsoid
-243 - 216*z - 18*x + 4*y^2 + 25*x^2 + 36*z^2 + 16*x*y = 0
- Imaginary Ellipsoid
2*x^2+4*y^2+z^2-4*x*y-4*y-2*z+5=0
- Double Hyperboloid
x^2+y^2-z^2-2*x-2*y+2*z+2=0
- Elliptical Paraboloid
x^2+y^2-6*x+6*y-4*z+18=0
- Two Parallel Planes
x^2+4*y^2+9*z^2+4*x*y+12*y*z+6*x*z-4*x-8*y-12*z+3=0
- Equation of imaginary intersecting lines
x^2 + 4*y^2 = 0
- Hyperbola equation
xy = 1
- Imaginary parallel lines
x^2 - 2x + 17 = 0
- Coincident straight lines
x^2 = 0
y^2 = 0
- Canonical Ellipsoid Equation
x^2/4 + y^2/9 + z^2 = 16
z^2 - 6*z - x/2 + y^2/9 + 25*x^2/36 + 4*x*y/9 - 27/4 = 0
- Imaginary cone
z^2 + y^2/9 + 25*x^2/36 + 4*x*y/9 - 6*z = 0
- One-sheeted hyperboloid
x^2/4 - y^2/9 + z^2 = 16
z^2 + x^2/4 + 2*y/9 + 5*y^2/36 - x*y/2 = 145/9
- Canonical cone equation
x^2/4 - y^2/9 + z^2 = 0
8*y + 36*z^2 + 18*x*y = 4 + 13*y^2 + 9*x^2
- Hyperbolic paraboloid
x^2/4 - y^2/9 = 2*z
4*x^2 + 4*z^2 + 2*y = y^2 + 8*x*z + 32*z + 33
xy = z
- Elliptical cylinder
16*x^2 + 25*y^2 - 32*x + 50*y - 359 = 0
x^2 + y^2 - 2x - 2y = 7
- Imaginary elliptical cylinder
5*x^2 + 13*y^2 + 70 = 0
25 - 16*y + 4*y^2 + 16*x^2 + 16*z^2 - 32*x*z = 0
- Intersecting planes
x^2 - y^2 = 0
16*x^2 - 25*y^2 + 16*z^2 - 32*x*z + 100*y - 100
- Hyperbolic cylinder
4*x^2 - 5*y^2 - 8*x + 20*y = 11
xy = 1
- Intersecting planes
x^2/4 - y^2/16 = 0
-100 - 4*y^2 + 16*x^2 + 16*z^2 + 40*y - 32*x*z
- Parabolic cylinder
y^2 = 2x
x^2 = -4y
-z^2/9 = x
y = sqrt(2)/2*z^2
10 + y^2 + z^2 - 2*x - 2*y*z
- Imaginary parallel planes
x^2 + 1 = 0
y^2 + 4 = 0
16 + 4*z^2 + 9*y^2 + 16*x^2 - 16*x*z - 12*y*z + 24*x*y = 0
- Coincident planes
y^2 = 0
x^2 = 0
4*x^2 + 9*y^2 + 16*z^2 - 24*y*z - 16*x*z + 12*x*y
Learn more about Canonical form
.
Examples of equations of lines and surfaces of the second order
| Equation | Canonical form | Type | Measurement |
|---|---|---|---|
| 9x^2+12xy+4y^2-24x-16y+3=0 | x^2=1 | Two parallel straight lines | Line |
| x^2-2xy+y^2-10x-6y+25=0 | y^2=4*sqrt(2)*x | Parabola | Line |
| 5x^2+4xy+y^2-6x-2y+2=0 | x^2/(1/sqrt(2*sqrt(2)+3))^2 + y^2/(1/sqrt(-2*sqrt(2)+3))^2=0 | Degenerate Ellipse | Line |
| 5*x^2+4*x*y+8*y^2+8*x+14*y+5=0 | x^2/(3/4)^2+y^2/(1/2)^2=1 | Ellipse | Line |
| 2*x^2+4*y^2+z^2-4*x*y-4*y-2*z+5=0 | z^2/(2/sqrt(2)/sqrt(3-sqrt(5)))^2+x^2/(2/sqrt(2)/sqrt(3+sqrt(5)))^2+y^2/(2/sqrt(2))^2=-1 | Imaginary Ellipsoid | Surface |
| x^2+y^2-z^2-2*x-2*y+2*z+2=0 | x^2/1^2+y^2-z^2=-1 | Double Hyperboloid | Surface |
| x^2+y^2-6*x+6*y-4*z+18=0 | x^2/2+y^2-2*z=0 or x^2/2+y^2+2*z=0 | Elliptical Paraboloid | Surface |
| x^2+4*y^2+9*z^2+4*x*y+12*y*z+6*x*z-4*x-8*y-12*z+3=0 | x^2/=1/14 | Two Parallel Planes | Surface |