Pārveidot kanoniskā veidā
Ar pareizu risinājumu kļūsi par visiem mīļāko grupā ❤️😊
Ko prot kanoniskā veida kalkulators?
- Pēc dotā vienādojuma atrod:
- Vienādojuma kanonisko veidu (2. kārtas līnijām un virsmām)
- Kanoniskās koordinātu sistēmas bāzes vektorus (2. kārtas līnijām)
- Kanoniskās koordinātu sistēmas centru (2. kārtas līnijām)
- Detalizēts risinājums divos veidos:
- Tiešā metode ar pāreju uz jaunu koordinātu centru un rotāciju ap jauno centru (līnijām)
- Invariantu metode ar daudzu determinantu aprēķinu (līnijām un virsmām)
- Zīmē 2. kārtas līnijas grafiku, kanoniskās sistēmas centru un bāzes vektorus
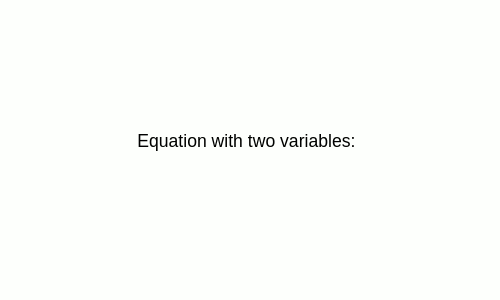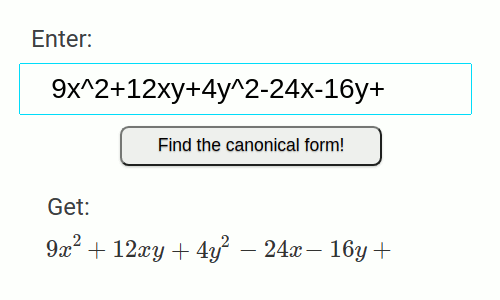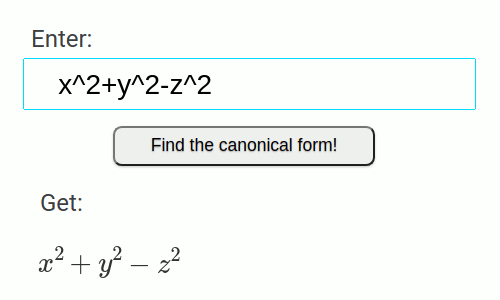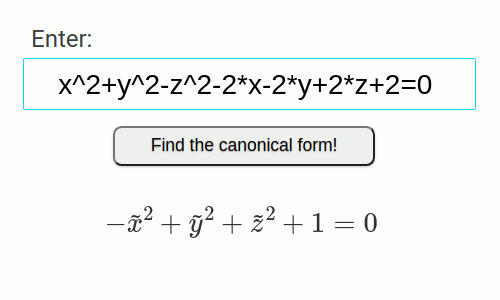
Piemēri
- Divas paralēlas taisnes
9x^2+12xy+4y^2-24x-16y+3=0
- Parabola
x^2-2xy+y^2-10x-6y+25=0
- Iznīcis elipse
5x^2+4xy+y^2-6x-2y+2=0
- Elipse
5*x^2+4*x*y+8*y^2+8*x+14*y+5=0
- Iztēles elipse
8063 - 250*y - 10*x + 50*x^2 + 50*y^2
- Elipsoīds
-243 - 216*z - 18*x + 4*y^2 + 25*x^2 + 36*z^2 + 16*x*y = 0
- Iztēlots elipsoīds
2*x^2+4*y^2+z^2-4*x*y-4*y-2*z+5=0
- Divslīpju hiperboloīds
x^2+y^2-z^2-2*x-2*y+2*z+2=0
- Eliptiskais paraboloīds
x^2+y^2-6*x+6*y-4*z+18=0
- Divas paralēlas plaknes
x^2+4*y^2+9*z^2+4*x*y+12*y*z+6*x*z-4*x-8*y-12*z+3=0
- Imagināro krustojošo taisņu vienādojums
x^2 + 4*y^2 = 0
- Hiperbolas vienādojums
xy = 1
- Imagināras paralēlās taisnes
x^2 - 2x + 17 = 0
- Sakrītošas taisnes
x^2 = 0
y^2 = 0
- Elipsoīda kanoniskais vienādojums
x^2/4 + y^2/9 + z^2 = 16
z^2 - 6*z - x/2 + y^2/9 + 25*x^2/36 + 4*x*y/9 - 27/4 = 0
- Imaginārs konuss
z^2 + y^2/9 + 25*x^2/36 + 4*x*y/9 - 6*z = 0
- Vienlapu hiperboloīds
x^2/4 - y^2/9 + z^2 = 16
z^2 + x^2/4 + 2*y/9 + 5*y^2/36 - x*y/2 = 145/9
- Konusa kanoniskais vienādojums
x^2/4 - y^2/9 + z^2 = 0
8*y + 36*z^2 + 18*x*y = 4 + 13*y^2 + 9*x^2
- Hiperboliskais paraboloīds
x^2/4 - y^2/9 = 2*z
4*x^2 + 4*z^2 + 2*y = y^2 + 8*x*z + 32*z + 33
xy = z
- Eliptiskais cilindrs
16*x^2 + 25*y^2 - 32*x + 50*y - 359 = 0
x^2 + y^2 - 2x - 2y = 7
- Imaginārais eliptiskais cilindrs
5*x^2 + 13*y^2 + 70 = 0
25 - 16*y + 4*y^2 + 16*x^2 + 16*z^2 - 32*x*z = 0
- Krustojošās plaknes
x^2 - y^2 = 0
16*x^2 - 25*y^2 + 16*z^2 - 32*x*z + 100*y - 100
- Hiperboliskais cilindrs
4*x^2 - 5*y^2 - 8*x + 20*y = 11
xy = 1
- Krustojošās plaknes
x^2/4 - y^2/16 = 0
-100 - 4*y^2 + 16*x^2 + 16*z^2 + 40*y - 32*x*z
- Paraboliskais cilindrs
y^2 = 2x
x^2 = -4y
-z^2/9 = x
y = sqrt(2)/2*z^2
10 + y^2 + z^2 - 2*x - 2*y*z
- Imaginārās paralēlās plaknes
x^2 + 1 = 0
y^2 + 4 = 0
16 + 4*z^2 + 9*y^2 + 16*x^2 - 16*x*z - 12*y*z + 24*x*y = 0
- Sakrītošās plaknes
y^2 = 0
x^2 = 0
4*x^2 + 9*y^2 + 16*z^2 - 24*y*z - 16*x*z + 12*x*y
Vairāk par Kanoniskais veids
.
2. kārtas līniju un virsmu vienādojumu piemēri
| Vienādojums | Kanoniskais veids | Tips | Dimensija |
|---|---|---|---|
| 9x^2+12xy+4y^2-24x-16y+3=0 | x^2=1 | Divas paralēlas taisnes | Līnija |
| x^2-2xy+y^2-10x-6y+25=0 | y^2=4*sqrt(2)*x | Parabola | Līnija |
| 5x^2+4xy+y^2-6x-2y+2=0 | x^2/(1/sqrt(2*sqrt(2)+3))^2 + y^2/(1/sqrt(-2*sqrt(2)+3))^2=0 | Iznīcis elipse | Līnija |
| 5*x^2+4*x*y+8*y^2+8*x+14*y+5=0 | x^2/(3/4)^2+y^2/(1/2)^2=1 | Elipse | Līnija |
| 2*x^2+4*y^2+z^2-4*x*y-4*y-2*z+5=0 | z^2/(2/sqrt(2)/sqrt(3-sqrt(5)))^2+x^2/(2/sqrt(2)/sqrt(3+sqrt(5)))^2+y^2/(2/sqrt(2))^2=-1 | Iztēlots elipsoīds | Virsma |
| x^2+y^2-z^2-2*x-2*y+2*z+2=0 | x^2/1^2+y^2-z^2=-1 | Divslīpju hiperboloīds | Virsma |
| x^2+y^2-6*x+6*y-4*z+18=0 | x^2/2+y^2-2*z=0 vai x^2/2+y^2+2*z=0 | Eliptiskais paraboloīds | Virsma |
| x^2+4*y^2+9*z^2+4*x*y+12*y*z+6*x*z-4*x-8*y-12*z+3=0 | x^2/=1/14 | Divas paralēlas plaknes | Virsma |
