Mister Exam
Other calculators
-
How to use it?
- Equation:
-
Equation 2x^2-8=0
-
Equation x^2-3x+5=0
-
Equation x^2+10*x+24=0
-
Equation (x-8)^2=(x-2)^2
- Express {x} in terms of y where:
- -14*x-3*y=-14
- 4*x-8*y=10
- 18*x-7*y=3
- -13*x+16*y=18
- Graphing y =:
- x^2+7
- Derivative of:
-
x^2+7
-
8*x
- Integral of d{x}:
-
x^2+7
- 8*x
- 8*x
-
Identical expressions
- x^ two + seven = eight *x
- x squared plus 7 equally 8 multiply by x
- x to the power of two plus seven equally eight multiply by x
- x2+7=8*x
- x²+7=8*x
- x to the power of 2+7=8*x
- x^2+7=8x
- x2+7=8x
-
Similar expressions
- 2x^2-8x+11=0
- x^2-7=8*x
- 16x^3+8x^2+x=0
- 6x^2=48x
x^2+7=8*x equation
The teacher will be very surprised to see your correct solution 😉
The solution
Detail solution
Move right part of the equation to
left part with negative sign.
The equation is transformed from
$$x^{2} + 7 = 8 x$$
to
$$- 8 x + \left(x^{2} + 7\right) = 0$$
This equation is of the form
A quadratic equation can be solved
using the discriminant.
The roots of the quadratic equation:
$$x_{1} = \frac{\sqrt{D} - b}{2 a}$$
$$x_{2} = \frac{- \sqrt{D} - b}{2 a}$$
where D = b^2 - 4*a*c - it is the discriminant.
Because
$$a = 1$$
$$b = -8$$
$$c = 7$$
, then
Because D > 0, then the equation has two roots.
or
$$x_{1} = 7$$
$$x_{2} = 1$$
left part with negative sign.
The equation is transformed from
$$x^{2} + 7 = 8 x$$
to
$$- 8 x + \left(x^{2} + 7\right) = 0$$
This equation is of the form
a*x^2 + b*x + c = 0
A quadratic equation can be solved
using the discriminant.
The roots of the quadratic equation:
$$x_{1} = \frac{\sqrt{D} - b}{2 a}$$
$$x_{2} = \frac{- \sqrt{D} - b}{2 a}$$
where D = b^2 - 4*a*c - it is the discriminant.
Because
$$a = 1$$
$$b = -8$$
$$c = 7$$
, then
D = b^2 - 4 * a * c =
(-8)^2 - 4 * (1) * (7) = 36
Because D > 0, then the equation has two roots.
x1 = (-b + sqrt(D)) / (2*a)
x2 = (-b - sqrt(D)) / (2*a)
or
$$x_{1} = 7$$
$$x_{2} = 1$$
Vieta's Theorem
it is reduced quadratic equation
$$p x + q + x^{2} = 0$$
where
$$p = \frac{b}{a}$$
$$p = -8$$
$$q = \frac{c}{a}$$
$$q = 7$$
Vieta Formulas
$$x_{1} + x_{2} = - p$$
$$x_{1} x_{2} = q$$
$$x_{1} + x_{2} = 8$$
$$x_{1} x_{2} = 7$$
$$p x + q + x^{2} = 0$$
where
$$p = \frac{b}{a}$$
$$p = -8$$
$$q = \frac{c}{a}$$
$$q = 7$$
Vieta Formulas
$$x_{1} + x_{2} = - p$$
$$x_{1} x_{2} = q$$
$$x_{1} + x_{2} = 8$$
$$x_{1} x_{2} = 7$$
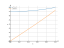
The graph