sqrt(3-x)=x+1 equation
The teacher will be very surprised to see your correct solution 😉
The solution
Detail solution
Given the equation
$$\sqrt{3 - x} = x + 1$$
$$\sqrt{3 - x} = x + 1$$
We raise the equation sides to 2-th degree
$$3 - x = \left(x + 1\right)^{2}$$
$$3 - x = x^{2} + 2 x + 1$$
Transfer the right side of the equation left part with negative sign
$$- x^{2} - 3 x + 2 = 0$$
This equation is of the form
A quadratic equation can be solved
using the discriminant.
The roots of the quadratic equation:
$$x_{1} = \frac{\sqrt{D} - b}{2 a}$$
$$x_{2} = \frac{- \sqrt{D} - b}{2 a}$$
where D = b^2 - 4*a*c - it is the discriminant.
Because
$$a = -1$$
$$b = -3$$
$$c = 2$$
, then
Because D > 0, then the equation has two roots.
or
$$x_{1} = - \frac{\sqrt{17}}{2} - \frac{3}{2}$$
$$x_{2} = - \frac{3}{2} + \frac{\sqrt{17}}{2}$$
Because
$$\sqrt{3 - x} = x + 1$$
and
$$\sqrt{3 - x} \geq 0$$
then
$$x + 1 \geq 0$$
or
$$-1 \leq x$$
$$x < \infty$$
The final answer:
$$x_{2} = - \frac{3}{2} + \frac{\sqrt{17}}{2}$$
$$\sqrt{3 - x} = x + 1$$
$$\sqrt{3 - x} = x + 1$$
We raise the equation sides to 2-th degree
$$3 - x = \left(x + 1\right)^{2}$$
$$3 - x = x^{2} + 2 x + 1$$
Transfer the right side of the equation left part with negative sign
$$- x^{2} - 3 x + 2 = 0$$
This equation is of the form
a*x^2 + b*x + c = 0
A quadratic equation can be solved
using the discriminant.
The roots of the quadratic equation:
$$x_{1} = \frac{\sqrt{D} - b}{2 a}$$
$$x_{2} = \frac{- \sqrt{D} - b}{2 a}$$
where D = b^2 - 4*a*c - it is the discriminant.
Because
$$a = -1$$
$$b = -3$$
$$c = 2$$
, then
D = b^2 - 4 * a * c =
(-3)^2 - 4 * (-1) * (2) = 17
Because D > 0, then the equation has two roots.
x1 = (-b + sqrt(D)) / (2*a)
x2 = (-b - sqrt(D)) / (2*a)
or
$$x_{1} = - \frac{\sqrt{17}}{2} - \frac{3}{2}$$
$$x_{2} = - \frac{3}{2} + \frac{\sqrt{17}}{2}$$
Because
$$\sqrt{3 - x} = x + 1$$
and
$$\sqrt{3 - x} \geq 0$$
then
$$x + 1 \geq 0$$
or
$$-1 \leq x$$
$$x < \infty$$
The final answer:
$$x_{2} = - \frac{3}{2} + \frac{\sqrt{17}}{2}$$
Rapid solution
[src]
____
3 \/ 17
x1 = - - + ------
2 2
$$x_{1} = - \frac{3}{2} + \frac{\sqrt{17}}{2}$$
x1 = -3/2 + sqrt(17)/2
Sum and product of roots
[src]
sum
____ 3 \/ 17 - - + ------ 2 2
$$- \frac{3}{2} + \frac{\sqrt{17}}{2}$$
=
____ 3 \/ 17 - - + ------ 2 2
$$- \frac{3}{2} + \frac{\sqrt{17}}{2}$$
product
____ 3 \/ 17 - - + ------ 2 2
$$- \frac{3}{2} + \frac{\sqrt{17}}{2}$$
=
____ 3 \/ 17 - - + ------ 2 2
$$- \frac{3}{2} + \frac{\sqrt{17}}{2}$$
-3/2 + sqrt(17)/2

 Equation -7x=4
Equation -7x=4
 Equation x^2-6=0
Equation x^2-6=0
 Equation x^2+7*x+12=0
Equation x^2+7*x+12=0
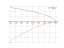 sqrt(3-x)
sqrt(3-x)
 sqrt(3-x)
sqrt(3-x)
 x+1
x+1
 sqrt(3-x)
sqrt(3-x)